题目内容
1.已知函数f(x)=x2-4|x|+3.(1)试证明函数f(x)是偶函数;
(2)画出f(x)的图象;(要求先用铅笔画出草图,再用中性笔描摹)
(3)请根据图象指出函数f(x)的单调递增区间与单调递减区间;(不必证明)
(4)当实数k取不同的值时,讨论关于x的方程x2-4|x|+3=k的实根的个数.
分析 (1)根据函数的定义域为R,关于原点对称,且满足f(-x)=f(x),可得函数 f(x)是偶函数.
(2)先去绝对值,然后根据二次函数、分段函数图象的画法画出函数f(x)的图象.
(3)通过图象即可求得f(x)的单调递增和递减区间;
(4)通过图象即可得到k的取值和对应的原方程实根的个数.
解答 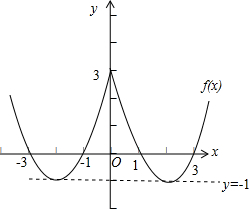 解:(1)由于函数f(x)=x2-4|x|+3的定义域为R,
解:(1)由于函数f(x)=x2-4|x|+3的定义域为R,
关于原点对称,
且满足f(-x)=(-x)2-4|-x|+3=x2-4|x|+3=f(x),
故函数 f(x)是偶函数.
(2)f(x)的图象如图所示:
(3)根据图象指出函数f(x)的单调递增区间
为[-2,0]、[2,+∞);
单调递减区间为(-∞,-2]、[0,2].
(4)当实数k取不同的值时,
讨论关于x的方程x2-4|x|+3=k的实根的个数,
即函数y=x2-4|x|+3的图象和直线y=k交点的个数.
由图象可看出,当k<-1时,方程实根的个数为0;
当k=-1时,方程实根的个数为2;
当-1<k<3时,方程实根个数为4;
当k=3时,方程实根个数为3;
当k>3时,方程实根个数为2.
点评 本题主要考查含绝对值函数的处理方法:去绝对值,二次函数、分段函数图象的画法,函数单调性的定义,以及根据图象写出函数的单调区间,数形结合讨论方程实根个数的方法,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
10.某设备的使用年限x(单位:年)与所支付的维修费用y(单位:千元)的一组数据如表:
从散点图分析.Y与x线性相关,根据上表中数据可得其线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{b}$=1.54.由此预测该设备的使用年限为6年时需支付的维修费用约是( )
| 使用年限x | 2 | 3 | 4 | 5 |
| 维修费用y | 2 | 3.4 | 5 | 6.6 |
| A. | 7.2千元 | B. | 7.8千元 | C. | 8.1千元 | D. | 9.5千元 |
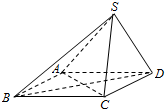 已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.
已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.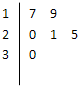 某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.
某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.