题目内容
15. 如图AB是圆O的一条弦,过点A作圆的切线AD,作BC⊥AC,与该圆交于点D,若AC=2$\sqrt{3}$,CD=2.
如图AB是圆O的一条弦,过点A作圆的切线AD,作BC⊥AC,与该圆交于点D,若AC=2$\sqrt{3}$,CD=2.(1)求圆O的半径;
(2)若点E为AB中点,求证O,E,D三点共线.
分析 (1)取BD中点为F,连结OF,求出BC,可得BF,利用勾股定理求圆O的半径;
(2)证明四边形OADB为平行四边形,利用E为AB的中点,即可证明O,E,D三点共线.
解答  (1)解:取BD中点为F,连结OF,由题意知,OF∥AC,OF=AC.
(1)解:取BD中点为F,连结OF,由题意知,OF∥AC,OF=AC.
∵AC为圆O的切线,BC为割线,
∴CA2=CD•CB,
由$AC=2\sqrt{3},CD=2$,∴BC=6,
∴BD=4,BF=2
在Rt△OBF中,由勾股定理得,$r=OB=\sqrt{O{F^2}+B{F^2}}=4$.(5分)
(2)证明:由(1)知,OA∥BD,OA=BD
∴四边形OADB为平行四边形,
又∵E为AB的中点,
∴OD与AB交于点E,
∴O,E,D三点共线.(5分)
点评 本小题主要考查平面几何的证明,具体涉及到圆的切线的性质,切割线定理等内容.本小题重点考查考生对平面几何推理能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.已知点P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)右支上的动点,F1、F2分别是双曲线的左、右焦点,∠F1PF2的角平分线l与x轴交于点Q(x0,0),设双曲线的半焦距为c,若x0的范围是0<x0≤$\frac{2}{3}$c,则双曲线的离心率是( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
7.某地区有小学18所,中学12所,大学6所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,求抽取的2所学校均为小学的概率;
(2)若某小学被抽取,该小学五个年级近视眼率y的数据如下表:
根据前四个年级的数据,利用最小二乘法求y关于x的线性回归直线方程,并计算五年级近视眼率的估计值与实际值之间的差的绝对值.
(附:回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
(1)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,求抽取的2所学校均为小学的概率;
(2)若某小学被抽取,该小学五个年级近视眼率y的数据如下表:
| 年级号x | 1 | 2 | 3 | 4 | 5 |
| 近视眼率y | 0.1 | 0.15 | 0.2 | 0.3 | 0.39 |
(附:回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
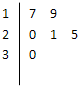 某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.
某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.