题目内容
19.直线l1:ρsin(θ+α)=a和l2:θ=$\frac{π}{2}$-α的位置关系是( )| A. | l1∥l2 | B. | l1⊥l2 | C. | l1和l2重合 | D. | l1,l2斜交 |
分析 把直线的极坐标方程化为直角坐标方程,利用直线垂直与斜率的关系即可得出.
解答 解:①α≠$\frac{π}{2}$时,直线l1:ρsin(θ+α)=a化为ρcosθsinα+ρsinθcosα=a,
∴xsinα+ycosα=a,其斜率k=-$\frac{sinα}{cosα}$=-tanα,
又直线l2:θ=$\frac{π}{2}$-α,∴斜率k′=tan($\frac{π}{2}$-α)=$\frac{1}{tanα}$,
∴k′k=-1,∴l1⊥l2.
②α=$\frac{π}{2}$,直线l1:ρsin(θ+α)=a化为ρcosθ=a,即x=a,
又直线l2:θ=$\frac{π}{2}$-α,化为θ=0,即k'=0,
∴l1⊥l2.
综上可得:l1⊥l2.
故选;B.
点评 本题考查了把直线的极坐标方程化为直角坐标方程、直线垂直与斜率的关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.某地区有小学18所,中学12所,大学6所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,求抽取的2所学校均为小学的概率;
(2)若某小学被抽取,该小学五个年级近视眼率y的数据如下表:
根据前四个年级的数据,利用最小二乘法求y关于x的线性回归直线方程,并计算五年级近视眼率的估计值与实际值之间的差的绝对值.
(附:回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
(1)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,求抽取的2所学校均为小学的概率;
(2)若某小学被抽取,该小学五个年级近视眼率y的数据如下表:
| 年级号x | 1 | 2 | 3 | 4 | 5 |
| 近视眼率y | 0.1 | 0.15 | 0.2 | 0.3 | 0.39 |
(附:回归直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的斜率和截距的最小二乘法估计公式分别为:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
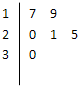 某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.
某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.