题目内容
19.如图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是( )
| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | 5 |
分析 根据三视图得出:空间几何体的性质得出直线平面的垂直问题,判断各个线段的长度比较即可.
解答 解:∵根据三视图得出:几何体为下图
AD,AB,AG相互垂直,面AEFG⊥面ABCDE,
BC∥AE,AB=AD=AG=3,DE=1,
根据几何体的性质得出:AC=3$\sqrt{2}$,GC=$\sqrt{{3}^{2}+(3\sqrt{2})^{2}}$=$\sqrt{27}$=$3\sqrt{3}$,GE=$\sqrt{{3}^{2}+{4}^{2}}$=5,
BG=$3\sqrt{2}$,AD=4,EF=$\sqrt{10}$,CE=$\sqrt{10}$,
故最长的为GC=3$\sqrt{3}$
故选;B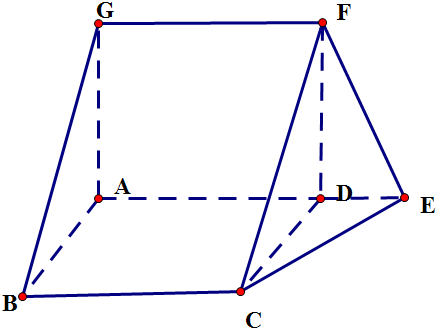
点评 本题考查了复杂几何体的三视图的运用,主要是恢复几何体的直观图,利用几何体的性质判断即可,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
10.某设备的使用年限x(单位:年)与所支付的维修费用y(单位:千元)的一组数据如表:
从散点图分析.Y与x线性相关,根据上表中数据可得其线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的$\widehat{b}$=1.54.由此预测该设备的使用年限为6年时需支付的维修费用约是( )
| 使用年限x | 2 | 3 | 4 | 5 |
| 维修费用y | 2 | 3.4 | 5 | 6.6 |
| A. | 7.2千元 | B. | 7.8千元 | C. | 8.1千元 | D. | 9.5千元 |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的菱形,且∠BAD=60°,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的菱形,且∠BAD=60°,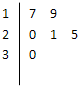 某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.
某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.