题目内容
5.已知在面积为3的△ABC所在的平面内有一点O满足丨$\overrightarrow{OB}$丨=2,且$\overrightarrow{OA}$-$\overrightarrow{OB}$+3$\overrightarrow{OC}$=0,若△OAB与△OBC的面积分别为S1,S2,则$\overrightarrow{OB}$•(S1$\overrightarrow{BC}$+S2$\overrightarrow{BA}$)=-12.分析 由已知,结合向量的基本运算可求得$\overrightarrow{AB}$=3$\overrightarrow{OC}$,从而可得AB∥OC,AB=3OC,可得,S1=S△OAB=S△ABC,
S2=S△OBC=$\frac{1}{3}$S△OAB,代入到所求式子即可求解
解答  解:∵$\overrightarrow{OA}$-$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$,即$\overrightarrow{AB}$=3$\overrightarrow{OC}$,
解:∵$\overrightarrow{OA}$-$\overrightarrow{OB}$+3$\overrightarrow{OC}$=$\overrightarrow{0}$,即$\overrightarrow{AB}$=3$\overrightarrow{OC}$,
∴AB∥OC,AB=3OC,如图所示:
由题意可得,S1=S△OAB=S△ABC=3,
由于点A到直线OB的距离等于点C到直线OB的距离的3倍,
∴S2=S△OBC=$\frac{1}{3}$S△OAB=1,
则$\overrightarrow{OB}$•(S1$\overrightarrow{BC}$+S2$\overrightarrow{BA}$)=$\overrightarrow{OB}$•(3$\overrightarrow{BC}$+$\overrightarrow{BA}$)=3$\overrightarrow{OB}•\overrightarrow{BC}$+$\overrightarrow{OB}$•$\overrightarrow{BA}$
=3$\overrightarrow{OB}•\overrightarrow{BC}$-3$\overrightarrow{OB}•\overrightarrow{OC}$=3($\overrightarrow{BC}+\overrightarrow{CO}$)$•\overrightarrow{OB}$=-3${\overrightarrow{OB}}^{2}$=-12
故答案为:-12
点评 本题主要考查了向量的基本运算及向量的数量积的基本运算,求解的关键是准确求出已知图象的面积.

 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的菱形,且∠BAD=60°,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为1的菱形,且∠BAD=60°,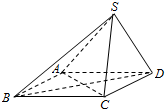 已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.
已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.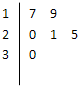 某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.
某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.