题目内容
2.已知$\frac{2}{5}$=$\frac{1}{3}$+$\frac{1}{15}$,
$\frac{2}{7}$=$\frac{1}{4}$+$\frac{1}{28}$,
$\frac{2}{9}$=$\frac{1}{5}$+$\frac{1}{45}$,
…
观察以上各等式有:n≥3,且n∈N*时,$\frac{2}{2n-1}$=$\frac{1}{n}+\frac{1}{n(2n-1)}$(n≥3,且n∈N*).
分析 找到已知中前三个式子,分析等号右边两项分母的变化规律,即可得到答案.
解答 解:∵已知
$\frac{2}{5}$=$\frac{1}{3}$+$\frac{1}{15}$=$\frac{1}{3}+\frac{1}{3×5}$,
$\frac{2}{7}$=$\frac{1}{4}$+$\frac{1}{28}$=$\frac{1}{4}+\frac{1}{4×7}$,
$\frac{2}{9}$=$\frac{1}{5}$+$\frac{1}{45}$=$\frac{1}{5}+\frac{1}{5×9}$,
…
归纳可得,
$\frac{2}{2n-1}$=$\frac{1}{n}+\frac{1}{n(2n-1)}$(n≥3,且n∈N*)
故答案为:$\frac{1}{n}+\frac{1}{n(2n-1)}$(n≥3,且n∈N*)
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
13.下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A. | y=x+1 | B. | y=tanx | C. | y=log2x | D. | y=x3 |
17.已知某几何体的三视图如图所示,则该几何体的体积为( )
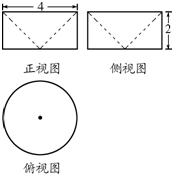

| A. | $\frac{8}{3}$π | B. | $\frac{16}{3}$π | C. | 8π | D. | 16π |
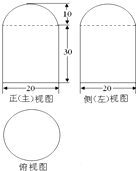
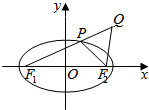 已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.
已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0. 如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.
如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.