题目内容
13.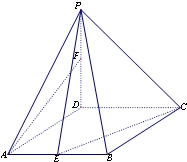 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.(1)求证:直线AF∥平面PEC;
(2)求证:AC⊥平面PBD;
(3)求PE与平面PDB所成角的正弦值.
分析 (1)利用中点问题,得出直线的平行AF∥EM,利用直线平面的平行问题求解证明即可.
(2)根据几何图形得出AC⊥BD,直线平面的垂直得出PD⊥AC,再运用判定定理求解证明即可.
(3)运用直线平面所成角的定义得出夹角,转化为直角三角形中求解即可.
解答 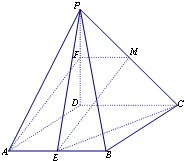 解:(1)证明:作FM∥CD交PC于M.
解:(1)证明:作FM∥CD交PC于M.
∵点F为PD中点,∴FM=$\frac{1}{2}CD$.
∵k=$\frac{1}{2}$,∴AE=$\frac{1}{2}AB$=FM,
∴AEMF为平行四边形,∴AF∥EM,
∵AF?平面PCE,EM?平面PEC,
∴直线AF∥平面PEC.
(2)∵底面ABCD是菱形,
∴AC⊥BD,
∵PD⊥平面ABCD,AC?平面ABCD,
∴PD⊥AC
∵PD∩BD=D,
∴AC⊥平面PBD;
(3)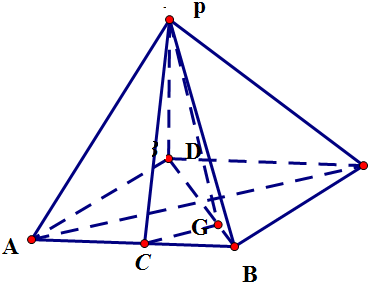
连接PE,PG
∵点E,O分别为AB和AC中点.
∴AO∥EG,
∵AC⊥平面PBD,
∴EG⊥平面PBD,
根据直线与平面所成角的定义可得:∠EPG为PE与平面PDB所成角,
Rt△EGP中,AO=$\frac{\sqrt{3}}{2}$,EG=$\frac{\sqrt{3}}{4}$,
DE=$\frac{\sqrt{3}}{2}$,PE=$\sqrt{{1}^{2}+\frac{3}{4}}$=$\frac{\sqrt{7}}{2}$,
∴sin∠EPG=$\frac{\frac{\sqrt{3}}{4}}{\frac{\sqrt{7}}{2}}$=$\frac{\sqrt{21}}{14}$,
∴PE与平面PDB所成角的正弦值=$\frac{\sqrt{21}}{14}$.
点评 本题考查了空间直线平面的平行,垂直,空间夹角问题,关键是熟练掌握定理,定义,把空间问题转化为平面问题求解,直线,直线,平面之间的转化问题.

| A. | [-6,2] | B. | [-6,0)∪( 0,2] | C. | [-2,0)∪( 0,6] | D. | (0,2] |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{6}}}{6}$ | D. | $\frac{{\sqrt{6}}}{8}$ |
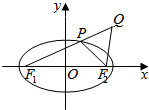 已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0.
已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1(a>b>0)的左、右焦点分别是F1,F2,Q是椭圆外的动点,满足|$\overrightarrow{{F}_{1}Q}$|=10.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足$\overrightarrow{PT}$•$\overrightarrow{T{F}_{2}}$=0,|$\overrightarrow{T{F}_{2}}$|=0. 如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.
如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.