题目内容
16. 如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.
如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.(1)证明△PBC为直角三角形;
(2)求直线AP与平面PBC所成角的正弦值.
分析 (1)建立空间坐标系,利用向量法即可证明△PBC为直角三角形;
(2)求出平面的法向量,利用向量法即可求直线AP与平面PBC所成角的正弦值.
解答 解:(1)以点E为坐标原点,以EB,EC所在的直线分别为x轴,y轴建立如图的空间直角坐标系E-xyz-----1’
则B($\sqrt{2}$,0,0),C(0,2,0),P(0,-1,$\sqrt{3}$)----2’
于是$\overrightarrow{BP}$=(-$\sqrt{2}$,-1,$\sqrt{3}$),$\overrightarrow{BC}$=(-$\sqrt{2}$,2,0),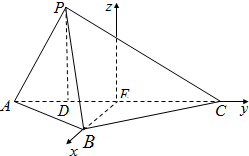
∵$\overrightarrow{BP}$•$\overrightarrow{BC}$=(-$\sqrt{2}$,-1,$\sqrt{3}$)•(-$\sqrt{2}$,2,0)=2-2=0,
∴$\overrightarrow{BP}$⊥$\overrightarrow{BC}$,
即BP⊥BC,-------------5’
∴△PBC为直角三角形------------------6’
(2)由(1)可得,A(0,-2,0)
于是$\overrightarrow{AP}$=(0,1,$\sqrt{3}$),---------------------7’
$\overrightarrow{PB}$=($\sqrt{2}$,1,-$\sqrt{3}$),$\overrightarrow{PC}$=(0,3,-$\sqrt{3}$),
设平面PBC的法向量为$\overrightarrow{n}$=(x,y,z)
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=0}\\{\overrightarrow{n}•\overrightarrow{PC}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{\sqrt{2}x+y-\sqrt{3}z=0}\\{3y-\sqrt{3}z=0}\end{array}\right.$,
取y=1,则z=$\sqrt{3}$,x=$\sqrt{2}$,
∴平面PBC的一个法向量为$\overrightarrow{n}$=($\sqrt{2}$,1,$\sqrt{3}$)-------------------------------------------10’
设直线AP与平面PBC所成的角为θ,
则sinθ=|cos<$\overrightarrow{AP}$,$\overrightarrow{n}$>|=$\frac{|\overrightarrow{AP}•\overrightarrow{n}|}{|\overrightarrow{AP}||\overrightarrow{n}|}$=$\frac{4}{2×\sqrt{6}}$=$\frac{\sqrt{6}}{3}$,
则θ=arcsin$\frac{\sqrt{6}}{3}$--------------12’
则直线AP与平面PBC所成角的大小为arcsin$\frac{\sqrt{6}}{3}$-------------------------------------13’
点评 本题主要考查空间向量的应用,建立空间坐标系,利用向量法是解决直线和平面所成角的基本方法,考查学生的运算能力.

 阅读快车系列答案
阅读快车系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | ($\frac{7}{24}$,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,+∞) | C. | ($\frac{1}{3}$,$\frac{2}{3}$] | D. | (0,$\frac{7}{24}$) |
 如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.
如图,在多面体ABCDEF中,底面ABCD是以AD,BC为腰的等腰梯形,且DC=$\frac{1}{2}AB,∠DAB={60°}$,EF∥AC,EF=$\frac{1}{2}$AC,M为AB的中点.