题目内容
【题目】[2019·朝鲜中学]在如图所示的程序框图中,有这样一个执行框![]() ,其中的函数关系式为
,其中的函数关系式为![]() ,程序框图中的
,程序框图中的![]() 为函数
为函数![]() 的定义域.
的定义域.

(1)若输入![]() ,请写出输出的所有
,请写出输出的所有![]() 的值;
的值;
(2)若输出的所有![]() 都相等,试求输入的初始值
都相等,试求输入的初始值![]() .
.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
⑴当![]() 时,可以求出
时,可以求出![]() ,满足条件
,满足条件![]() ,执行循环体,依此类推,而
,执行循环体,依此类推,而![]() ,不满足于条件,终止循环,解出
,不满足于条件,终止循环,解出![]() 的所有项即可
的所有项即可
⑵要使输出的所有![]() 都相等,根据程序框图可得
都相等,根据程序框图可得![]() ,解方程求出初始值
,解方程求出初始值![]() 的值即可
的值即可
(1)当x0=![]() 时,x1=f(x0)=f
时,x1=f(x0)=f![]() =
=![]() ,x2=f(x1)=f
,x2=f(x1)=f![]() =
=![]() ,
,
x3=f(x2)=f![]() =-1,终止循环.∴输出的数为
=-1,终止循环.∴输出的数为![]() ,
,![]() .
.
(2)要使输出的所有xi都相等,则xi=f(xi-1)=xi-1,此时有x1=f(x0)=x0,即![]() =x0,解得x0=1或x0=2,∴当输入的初始值x0=1或x0=2时,输出的所有xi都相等.
=x0,解得x0=1或x0=2,∴当输入的初始值x0=1或x0=2时,输出的所有xi都相等.

 阅读快车系列答案
阅读快车系列答案【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且圆
上,且圆![]() 经过点
经过点![]() 与点
与点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线,求切线所在的直线的方程.
的切线,求切线所在的直线的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)求出线段![]() 的中点
的中点![]() ,进而得到线段
,进而得到线段![]() 的垂直平分线为
的垂直平分线为![]() ,与
,与![]() 联立得交点
联立得交点![]() ,∴
,∴![]() .则圆
.则圆![]() 的方程可求
的方程可求
(2)当切线斜率不存在时,可知切线方程为![]() .
.
当切线斜率存在时,设切线方程为![]() ,由
,由![]() 到此直线的距离为
到此直线的距离为![]() ,解得
,解得![]() ,即可到切线所在直线的方程.
,即可到切线所在直线的方程.
试题解析:((1)设 线段![]() 的中点为
的中点为![]() ,∵
,∵![]() ,
,
∴线段![]() 的垂直平分线为
的垂直平分线为![]() ,与
,与![]() 联立得交点
联立得交点![]() ,
,
∴![]() .
.
∴圆![]() 的方程为
的方程为![]() .
.
(2)当切线斜率不存在时,切线方程为![]() .
.
当切线斜率存在时,设切线方程为![]() ,即
,即![]() ,
,
则![]() 到此直线的距离为
到此直线的距离为![]() ,解得
,解得![]() ,∴切线方程为
,∴切线方程为![]() .
.
故满足条件的切线方程为![]() 或
或![]() .
.
【点睛】本题考查圆的方程的求法,圆的切线,中点弦等问题,解题的关键是利用圆的特性,利用点到直线的距离公式求解.
【题型】解答题
【结束】
20
【题目】某小型企业甲产品生产的投入成本![]() (单位:万元)与产品销售收入
(单位:万元)与产品销售收入![]() (单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
(单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大(![]() )?
)?
相关公式: 
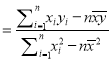 ,
, ![]() .
.