题目内容
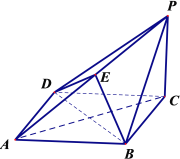
【题目】如图所示,正方形![]() 与直角梯形
与直角梯形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
, ![]() ,
, ![]() .
.
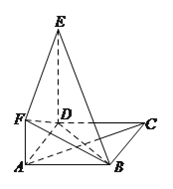
(I)求证: ![]() 平面
平面![]() .
.
(II)求证: ![]() 平面
平面![]() .
.
(III)求四面体![]() 的体积.
的体积.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)欲证AC⊥平面BDE,只需证明AC垂直平面BDE中的两条相交直线即可,因为AC与BD是正方形ABCD的对角线,所以AC⊥BD,再正DE垂直AC所在的平面,得到AC垂直DE,而BD,DE是平面BDE中的两条相交直线,问题得证.
(2)欲证AC∥平面BEF,只需证明AC平行平面BEF中的一条直线即可,利用中位线的性质证明OG平行DE且等于DE的一半,根据已知AF平行DE且等于DE的一半,所以OG与AF平行且相等,就可得到AC平行FG,而FG为平面BEF中的一条直线,问题得证.
(3)四面体BDEF可以看做以△DEF为底面,以点B为顶点的三棱锥,底面三角形DEF的底边DE=2,高DA=2,三棱锥的高为AB,长度等于2,再代入三棱锥的体积公式即可.
(![]() )因为平面
)因为平面![]() 平面
平面![]() ,
, ![]() ,
,
即![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 是正方形,所以
是正方形,所以![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() .
.
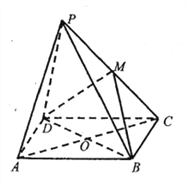
(![]() )设
)设![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,如下图:
,如下图:
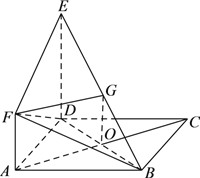
所以![]() 平行且等于
平行且等于![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() 平行且等于
平行且等于![]() ,从而四边形
,从而四边形![]() 是平行四边形,
是平行四边形,
![]() ,因为
,因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
即![]() 平面
平面![]() .
.
(![]() )
)![]() ,
, ![]() ,
,
因此四面体![]() 的体积
的体积![]() .
.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目