题目内容
【题目】已知椭圆C： 
+y2=1与直线l：y=kx+m相交于E、F两不同点，且直线l与圆O：x2+y2= 
相切于点W（O为坐标原点）．
（1）证明：OE⊥OF；
（2）设λ= 
，求实数λ的取值范围．
【答案】
（1）解：∵直线l与圆O相切，
∴圆x2+y2= 
的圆心到直线l的距离d= 
= 
，
∴ 
；
由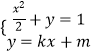 
，得：
（1+2k2）x2+4kmx+2m2﹣2=0；
设E（x1，y1），F（x2，y2），
则 
， 
；
∴ 
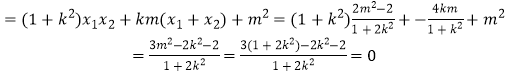
∴OE⊥OF；
（2）解：∵直线l与圆O相切于W， 
，
∴ 
；
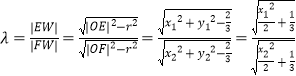由（1）知x1x2+y1y2=0，
∴x1x2=﹣y1y2，即 
；
从而 
，
即 
，
∴ 
；
∵﹣ 
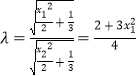≤x1≤ ，
∴λ∈[ 
，2]．
【解析】（1）由直线l与圆O相切，得圆心到直线l的距离d=r，再由直线l与椭圆C相交，得出E、F点的坐标关系，从而证明OE⊥OF；（2）根据直线l与圆O相切于点W，以及OE⊥OF，得出λ= 
的坐标表示，求出λ的取值范围．
练习册系列答案
相关题目
