题目内容
【题目】已知函数f(x)满足f(﹣x)=f(x),f(x+8)=f(x),且当x∈(0,4]时f(x)= ![]() ,关于x的不等式f2(x)+af(x)>0在[﹣2016,2016]上有且只有2016个整数解,则实数a的取值范围是( )
,关于x的不等式f2(x)+af(x)>0在[﹣2016,2016]上有且只有2016个整数解,则实数a的取值范围是( )
A.(﹣ ![]() ln6,ln2]
ln6,ln2]
B.(﹣ln2,﹣ ![]() ln6)
ln6)
C.(﹣ln2,﹣ ![]() ln6]
ln6]
D.(﹣ ![]() ln6,ln2)
ln6,ln2)
【答案】C
【解析】解:∵函数f(x)满足f(﹣x)=f(x),f(x+8)=f(x),
∴函数f(x)是偶函数,且周期是8,则在[﹣2016,2016]上共有504个周期,
∵不等式在[﹣2016,2016]上有且只有2016个整数解,∴在一个周期上有且只有4个整数解,
由偶函数的性质可得,在(0,4]上有且只有2个整数解,
∵当x∈(0,4]时f(x)= ![]() ,∴则f′(x)=
,∴则f′(x)= ![]() ,
,
当f′(x)>0得1﹣ln(2x)>0,即ln(2x)<1,
即0<2x<e,即0<x< ![]() ,
,
由f′(x)<0得1﹣ln(2x)<0,得ln(2x)>1,
即2x>e,即x> ![]() ,
,
即当x= ![]() 时,函数f(x)取得极大值,同时也是最大值
时,函数f(x)取得极大值,同时也是最大值
f( ![]() )=
)= ![]() =
= ![]() ,
,
即当0<x< ![]() 时,f(x)<
时,f(x)< ![]() 有一个整数解1,
有一个整数解1,
当x> ![]() 时,0<f(x)<
时,0<f(x)< ![]() 有无数个整数解,
有无数个整数解,
①若a=0,则f2(x)+af(x)>0得f2(x)>0,此时有无数个整数解,不满足条件.
②若a>0,
则由f2(x)+af(x)>0得f(x)>0或f(x)<﹣a,
当f(x)>0时,不等式由无数个整数解,不满足条件.
③当a<0时,由f2(x)+af(x)>0得f(x)>﹣a或f(x)<0,
当f(x)<0时,没有整数解,
则要使当f(x)>﹣a有两个整数解,
∵f(1)=ln2,f(2)= ![]() =ln2,f(3)=
=ln2,f(3)= ![]() ,
,
∴当f(x)≥ln2时,函数有两个整数点1,2,当f(x)≥ ![]() 时,函数有3个整数点1,2,3
时,函数有3个整数点1,2,3
∴要使f(x)>﹣a有两个整数解,
则 ![]() ≤﹣a<ln2,即﹣ln2<a≤﹣
≤﹣a<ln2,即﹣ln2<a≤﹣ ![]() ln6,
ln6,
故选:C.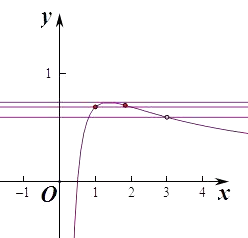

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案