题目内容
【题目】已知椭圆![]()
![]() 的右准线方程为
的右准线方程为![]() ,又离心率为
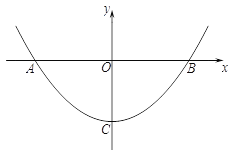
,又离心率为![]() ,椭圆的左顶点为
,椭圆的左顶点为![]() ,上顶点为
,上顶点为![]() ,点
,点![]() 为椭圆上异于
为椭圆上异于![]() 任意一点.
任意一点.
(1)求椭圆的方程;
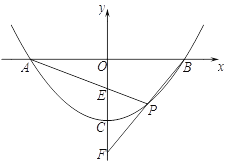
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)利用椭圆的准线方程和离心率即可求解;(2)设出点![]() 的坐标,写出的直线
的坐标,写出的直线![]() 方程,求出点
方程,求出点![]() 的坐标,利用两点间的距离公式和点
的坐标,利用两点间的距离公式和点![]() 在椭圆上进行化简求解.
在椭圆上进行化简求解.
试题解析:(1)∵椭圆的右准线方程为![]() ∴
∴![]() ∵离心率为
∵离心率为![]() ∴
∴![]()
∴![]() ∴
∴![]() ∴椭圆的方程为:
∴椭圆的方程为: ![]() ;
;
(2)方法(一)设点![]() ,则
,则![]() ,
, ![]() ,即
,即![]() .
.
当![]() 时,
时, ![]() ,则
,则![]() ,
, ![]() ∴
∴![]()
∵点![]() 异于点
异于点![]() ∴
∴![]()
当![]() 且
且![]() 时,设直线
时,设直线![]() 方程为:
方程为: ![]() ,它与
,它与![]() 轴交于点
轴交于点
直线![]() 方程为:
方程为: ![]() ,它与
,它与![]() 轴交于点
轴交于点
∴ ,
, 
∴
 为定值.
为定值.
方法(二)若直线![]() 斜率不存在,则直线
斜率不存在,则直线![]() 方程为:
方程为: ![]() ,此时
,此时![]() ,则
,则![]() ,
, ![]()
∴![]()
若直线![]() 斜率存在,设直线
斜率存在,设直线![]() 方程为:
方程为: ![]() ,且
,且![]()
∴![]() 且
且 
则联立方程:  得:
得: ![]() ,解得:
,解得: ![]() 或
或![]() ,
,
即点 ∵点
∵点![]() 异于点
异于点![]() ∴
∴![]()
∴
∴直线![]() 的方程为:
的方程为:  ,
,
则 且
且
∴ 为定值.
为定值.

【题目】[2019·朝鲜中学]在如图所示的程序框图中,有这样一个执行框![]() ,其中的函数关系式为
,其中的函数关系式为![]() ,程序框图中的
,程序框图中的![]() 为函数
为函数![]() 的定义域.
的定义域.

(1)若输入![]() ,请写出输出的所有
,请写出输出的所有![]() 的值;
的值;
(2)若输出的所有![]() 都相等,试求输入的初始值
都相等,试求输入的初始值![]() .
.
【题目】为了让学生更多地了解“数学史”知识,某班级举办一次“追寻先哲的足迹,倾听数学的声音的数学史知识竞赛活动.现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表:
序号 | 分数段 | 人数 | 频率 |
1 |
| 10 | 0.20 |
2 |
| ① | 0.44 |
3 |
| ② | ③ |
4 |
| 4 | 0.08 |
合计 | 50 | 1 | |
(1)填充上述表中的空格(在解答中直接写出对应空格序号的答案);
(2)若利用组中值近似计算数据的平均数,求此次数学史初赛的平均成绩;
(3)甲同学的初赛成绩在![]() ,学校为了宣传班级的学习经验,随机抽取分数在
,学校为了宣传班级的学习经验,随机抽取分数在![]() 的4位同学中的两位同学到学校其他班级介绍,求甲同学被抽取到的概率.
的4位同学中的两位同学到学校其他班级介绍,求甲同学被抽取到的概率.