题目内容
(本小题满分12分)等差数列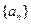 的前
的前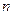 项和为
项和为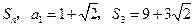 .
.
⑴求数列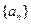 的通项
的通项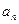 与前
与前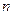 项和
项和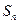 ;⑵设
;⑵设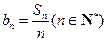 ,求证:数列
,求证:数列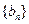 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
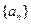 的前
的前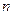 项和为
项和为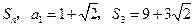 .
.⑴求数列
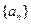 的通项
的通项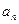 与前
与前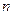 项和
项和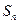 ;⑵设
;⑵设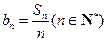 ,求证:数列
,求证:数列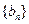 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.(Ⅰ)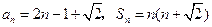 (Ⅱ)数列
(Ⅱ)数列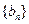 中任意不同的三项都不可能成等比数列.
中任意不同的三项都不可能成等比数列.
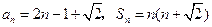 (Ⅱ)数列
(Ⅱ)数列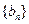 中任意不同的三项都不可能成等比数列.
中任意不同的三项都不可能成等比数列.(Ⅰ)由已知得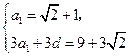 ,∴
,∴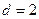 ,
, (3分)
(3分)
故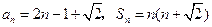 .
.  (5分)
(5分)
(Ⅱ)由(Ⅰ)得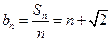 .
. 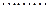 (6分)
(6分)
假设数列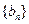 中存在三项
中存在三项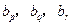 (
(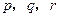 互不相等)成等比数列,
互不相等)成等比数列,
则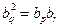 .即
.即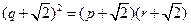 ,
,
∴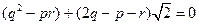
 (8分)
(8分)
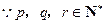 ,∴
,∴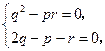 ∴
∴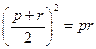 ,得
,得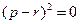 ,
,
∴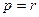 .与
.与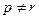 矛盾.
矛盾.  (10分)
(10分)
所以数列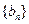 中任意不同的三项都不可能成等比数列.
中任意不同的三项都不可能成等比数列.  (12分)
(12分)
评析:(1)求解等差数列与等比数列的有关问题,定义、公式和性质是主要工具,要注意抓住基本量───首项和公差(公比),方程思想、化归思想和运算能力是考查的重点;
(2)正面求解,直接证明难以突破时,可以考虑从反面入手,运用正难则反的思想来处理,反证法就是从反面入手的一种重要的推理方法,一般地,以否定的形式出现的数学命题,我们常用反证法来实现证明。
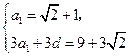 ,∴
,∴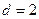 ,
,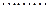 (3分)
(3分)故
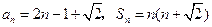 .
. 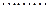 (5分)
(5分)(Ⅱ)由(Ⅰ)得
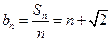 .
. 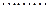 (6分)
(6分)假设数列
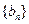 中存在三项
中存在三项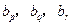 (
(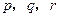 互不相等)成等比数列,
互不相等)成等比数列,则
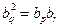 .即
.即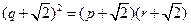 ,
,∴
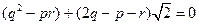
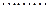 (8分)
(8分)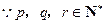 ,∴
,∴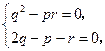 ∴
∴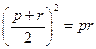 ,得
,得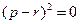 ,
,∴
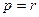 .与
.与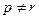 矛盾.
矛盾.  (10分)
(10分)所以数列
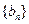 中任意不同的三项都不可能成等比数列.
中任意不同的三项都不可能成等比数列.  (12分)
(12分)评析:(1)求解等差数列与等比数列的有关问题,定义、公式和性质是主要工具,要注意抓住基本量───首项和公差(公比),方程思想、化归思想和运算能力是考查的重点;
(2)正面求解,直接证明难以突破时,可以考虑从反面入手,运用正难则反的思想来处理,反证法就是从反面入手的一种重要的推理方法,一般地,以否定的形式出现的数学命题,我们常用反证法来实现证明。

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,通项公式为
,通项公式为 ,
, .(Ⅰ)计算
.(Ⅰ)计算 的值;(Ⅱ)比较
的值;(Ⅱ)比较 与1的大小,并用数学归纳法证明你的结论.
与1的大小,并用数学归纳法证明你的结论.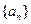 的公比为
的公比为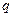 ,前
,前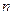 项和为
项和为 ,若
,若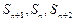 成等差数列,则
成等差数列,则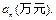
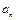 与n的关系式;
与n的关系式;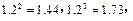
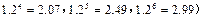
 是公差不为零的等差数列,
是公差不为零的等差数列,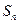 为其前
为其前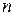 项和,满足
项和,满足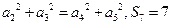 。(1)求数列
。(1)求数列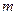 ,使得
,使得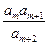 为数列
为数列
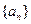 的前
的前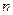 项和为
项和为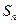 ,若
,若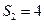 ,
,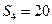 ,则该数列的公差
,则该数列的公差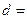 ( )
( )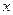 ,用
,用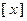 表示不超过
表示不超过 ,
,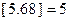 .若
.若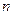 为正整数,
为正整数,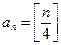 ,
,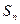 为数列
为数列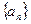 的前
的前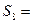 、
、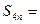 __________.
__________. 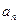 ﹜为等差数列,且
﹜为等差数列,且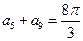 ,则
,则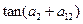 的值为
的值为