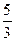题目内容
己知各项均为正数的数列{an}满足an+12+an+1an-2an2=0(n∈N*),且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式an;
(2)若bn=anlog
an,Sn=b1+b2+…+bn,求Sn+n•2n+1>50成立的正整数n的最小值.
(1)求数列{an}的通项公式an;
(2)若bn=anlog
| 1 |
| 2 |
(Ⅰ)∵an+12-an+1an-2an2=0,∴(an+1+an)(an+1-2an)=0,
∵数列{an}的各项均为正数,
∴an+1+an>0,
∴an+1-2an=0,
即an+1=2an,所以数列{an}是以2为公比的等比数列.
∵a3+2是a2,a4的等差中项,
∴a2+a4=2a3+4,
∴2a1+8a1=8a1+4,
∴a1=2,
∴数列{an}的通项公式an=2n.
(Ⅱ)由(Ⅰ)及bn=anlog
an得,bn=-n•2n,
∵Sn=b1+b2++bn,
∴Sn=-2-2•22-3•23-4•24--n•2n①
∴2Sn=-22-2•23-3•24-4•25--(n-1)•2n-n•2n+1②
①-②得,Sn=2+22+23+24+25++2n-n•2n+1
=
-n•2n+1=(1-n)•2n+1-2,
要使Sn+n•2n+1>50成立,只需2n+1-2>50成立,即2n+1>52,
∴使Sn+n•2n+1>50成立的正整数n的最小值为5.
∵数列{an}的各项均为正数,
∴an+1+an>0,
∴an+1-2an=0,
即an+1=2an,所以数列{an}是以2为公比的等比数列.
∵a3+2是a2,a4的等差中项,
∴a2+a4=2a3+4,
∴2a1+8a1=8a1+4,
∴a1=2,
∴数列{an}的通项公式an=2n.
(Ⅱ)由(Ⅰ)及bn=anlog
| 1 |
| 2 |
∵Sn=b1+b2++bn,
∴Sn=-2-2•22-3•23-4•24--n•2n①
∴2Sn=-22-2•23-3•24-4•25--(n-1)•2n-n•2n+1②
①-②得,Sn=2+22+23+24+25++2n-n•2n+1
=
| 2(1-2n) |
| 1-2 |
要使Sn+n•2n+1>50成立,只需2n+1-2>50成立,即2n+1>52,
∴使Sn+n•2n+1>50成立的正整数n的最小值为5.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
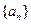 的前
的前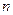 项和为
项和为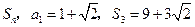 .
.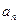 与前
与前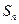 ;⑵设
;⑵设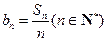 ,求证:数列
,求证:数列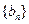 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.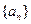 的前n项和为
的前n项和为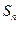 ,且
,且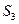 =6,
=6,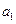 =4, 则公差d等于( )
=4, 则公差d等于( )