Question

椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的左右焦点分别为F₁，F₂，若椭圆C上恰好有6个不同的点P，使得△F₁F₂P为等腰三角形，则椭圆C的离心率的取值范围是（　　）

A．( 1 3 ， 2 3 )

B．( 1 2 ，1)

C．( 2 3 ，1)

D．( 1 3 ， 1 2 )∪( 1 2 ，1)

Answer 1

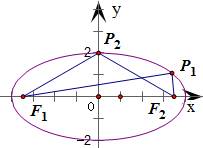
①当点P与短轴的顶点重合时，
△F₁F₂P构成以F₁F₂为底边的等腰三角形，
此种情况有2个满足条件的等腰△F₁F₂P；
②当△F₁F₂P构成以F₁F₂为一腰的等腰三角形时，
以F₂P作为等腰三角形的底边为例，
∵F₁F₂=F₁P，
∴点P在以F₁为圆心，半径为焦距2c的圆上
因此，当以F₁为圆心，半径为2c的圆与椭圆C有2交点时，
存在2个满足条件的等腰△F₁F₂P，
此时a-c＜2c，解得a＜3c，所以离心率e＞

1

3

当e=

1

2

时，△F₁F₂P是等边三角形，与①中的三角形重复，故e≠

1

2

同理，当F₁P为等腰三角形的底边时，在e＞

1

3

且e≠

1

2

时也存在2个满足条件的等腰△F₁F₂P
这样，总共有6个不同的点P使得△F₁F₂P为等腰三角形
综上所述，离心率的取值范围是：e∈（

1

3

，

1

2

）∪（

1

2

，1）