题目内容
椭圆
+
=1(a>b>0)的左焦点F到过顶点A(-a,0)、B(0,b)的直线的距离等于
b,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 7 |
A.
| B.
| C.
| D.
|
∵直线AB的方程为
+
=1,即bx-ay+ab=0(a>b>0),
∵左焦点F(-c,0)到AB的距离d等于
b,
即d=
=
b,
∴
=
,
∴
=
,又b2=a2-c2,
∴8c2-14ac+5a2=0,又e=
,
两端同除以a2得:8e2-14e+5=0,
解得:e=
或e=
(舍去).
∴椭圆的离心率为
.
故选A.
| x |
| -a |
| y |
| b |
∵左焦点F(-c,0)到AB的距离d等于
| ||
| 7 |
即d=
| |-bc+ab| | ||
|
| ||
| 7 |
∴
| |a-c| | ||
|
| ||
| 7 |
∴
| (a-c)2 |
| a2+b2 |
| 1 |
| 7 |
∴8c2-14ac+5a2=0,又e=
| c |
| a |
两端同除以a2得:8e2-14e+5=0,
解得:e=
| 1 |
| 2 |
| 5 |
| 4 |
∴椭圆的离心率为
| 1 |
| 2 |
故选A.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
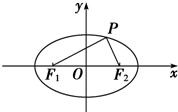

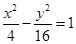 的渐近线方程为 .
的渐近线方程为 .