题目内容

（理）已知F1，F2是椭圆
x2
100
+
y2
64
=1的焦点，P为椭圆上一点，且∠F1PF2=
π
3
，求△F1PF2的面积．
依题意，作图如下：

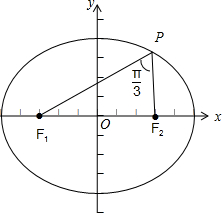
∵a=10，b=8，故c=
a2-b2
=6，
即|PF1|+|PF2|=2a=20，|F1F2|=2c=12，
又∠F1PF2=
π
3
，
∴由余弦定理得：|F1F2|2=|PF1|2+|PF2|2-2|PF1|•|PF2|cos∠F1PF2，
|F1F2|2=(|PF1|+|PF2|)2-2|PF1|•|PF2|-2|PF1|•|PF2|cos∠F1PF2，
即4c2=4a2-3|PF1|•|PF2|，
∴|PF1|•|PF2|=
256
3
，
∴S△F1PF2=
1
2
|PF1|•|PF2|sin∠F1PF2=
1
2
×
256
3
×
3
2
=
64
3
3
．
练习册系列答案
相关题目
已知A1，A2为椭圆
x2
4
+y2=1的左右顶点，在长轴A1A2上随机任取点M，过M作垂直于x轴的直线交椭圆于点P，则使∠PA1A2＜45°的概率为（　　）
A．
4
5
B．
7
10
C．
3
10
D．
1
5
点P是椭圆
x2
9
+
y2
4
=1上的一点，F1，F2是焦点，且∠F1PF2=60°，则△F1PF2的面积是（　　）
A．
4
3
3
B．4
3
C．
4
3
D．
3
2
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的焦点分别为F1，F2，若该椭圆上存在一点P使得∠F1PF2=60°，则椭圆离心率的取值范围是______．
已知椭圆C的左、右焦点坐标分别是(-
3
，0)，(
3
，0)，离心率是
3
2
，则椭圆C的方程为（　　）
A．
x2
2
+y2=1		B．
x2
4
+y2=1		C．x2+
y2
2
=1		D．x2+
y2
4
=1
若两集合A=[0，3]，B=[0，3]，分别从集合A、B中各任取一个元素m、n，即满足m∈A，n∈B，记为（m，n），
（Ⅰ）若m∈Z，n∈Z，写出所有的（m，n）的取值情况，并求事件“方程
x2
m+1
+
y2
n+1
=1所对应的曲线表示焦点在x轴上的椭圆”的概率；
（Ⅱ）求事件“方程
x2
m+1
+
y2
n+1
=1所对应的曲线表示焦点在x轴上的椭圆，且长轴长大于短轴长的
2
倍”的概率．
已知点A（-1，0）、B（1，0），P（x0，y0）是直线y=x+2上任意一点，以A、B为焦点的椭圆过点P．记椭圆离心率e关于x0的函数为e（x0），那么下列结论正确的是（　　）
A．e与x0一一对应
B．函数e（x0）无最小值，有最大值
C．函数e（x0）是增函数
D．函数e（x0）有最小值，无最大值
已知F1、F2是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的两个焦点，若椭圆上存在点P使
PF1
•
PF2
=0，则|PF1|•|PF2|=（　　）
A．b2B．2b2C．2bD．b
椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左右焦点分别为F1，F2，若椭圆C上恰好有6个不同的点P，使得△F1F2P为等腰三角形，则椭圆C的离心率的取值范围是（　　）
A．(
1
3
，
2
3
)		B．(
1
2
，1)		C．(
2
3
，1)		D．(
1
3
，
1
2
)∪(
1
2
，1)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网