题目内容
13.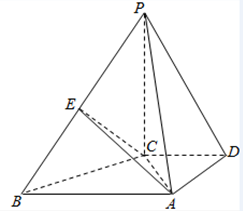 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.(1)证明:AC⊥平面PBC;
(2)若点P到平面ACE的距离为$\frac{\sqrt{6}}{3}$,求三棱椎P-ACD的体积.
分析 (1)取AB的中点M,连接CM,由已知可得:四边形CDAM是正方形,CM=MA=MB,可得AC⊥CB,PC⊥底面ABCD,于是PC⊥AC,即可证明AC⊥平面PBC;
(2)在平面PBC内作PH⊥CE,垂足为H.由(1)可得:平面PBC⊥平面PBC,在平面PBC内作PH⊥CE,垂足为H,可得PH⊥平面ACE,PH=$\frac{\sqrt{6}}{3}$.设PC=t,S△PCE=$\frac{1}{2}$S△PBC=$\frac{\sqrt{2}}{4}$t.又S△PCE=$\frac{1}{2}$CE•PH,解得t,即可得到VP-ACD=$\frac{1}{3}$•S△ACD•PC.
解答 (1)证明:取AB的中点M,连接CM,
∵AM=$\frac{1}{2}$AB=1=CD=AD,AB⊥AD,AB∥CD,
∴四边形CDAM是正方形,CM=MA=MB,
∴AC⊥CB,
∵PC⊥底面ABCD,
∴PC⊥AC,又PC∩BC=C,
∴AC⊥平面PBC;
(2)解:在平面PBC内作PH⊥CE,垂足为H.
由(1)可得:平面PBC⊥平面AEC,
在平面PBC内作PH⊥CE,垂足为H,则PH⊥平面ACE,
∴PH=$\frac{\sqrt{6}}{3}$.
设PC=t,则PB=$\sqrt{2+{t}^{2}}$,CE=$\frac{1}{2}$PB=$\frac{1}{2}\sqrt{2+{t}^{2}}$,
又S△PBC=$\frac{1}{2}$•$\sqrt{2}$t,S△PCE=$\frac{1}{2}$S△PBC=$\frac{\sqrt{2}}{4}$t.
由S△PCE=$\frac{1}{2}$CE•PH,
得$\frac{1}{2}$•$\frac{\sqrt{2+{t}^{2}}}{2}$•$\frac{\sqrt{6}}{3}$=$\frac{\sqrt{2}}{4}$t,解得t=1,即PC=1.
∴VP-ACD=$\frac{1}{3}$•S△ACD•PC=$\frac{1}{3}×\frac{1}{2}×1×1×1=\frac{1}{6}$.
点评 本小题主要考查空间线面关系、二面角的度量、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

| A. | 4种 | B. | 5种 | C. | 24种 | D. | 120种 |