题目内容
5.设i为虚数单位,n为正整数.试用数学归纳法证明(cosx+isinx)n=cosnx+isinnx.分析 利用数学归纳法即可证明.
解答 解:①当n=1时,左边=cosx+isinx=右边,此时等式成立;
②假设当n=k时,等式成立,即(cosx+isinx)k=coskx+isinkx.
则当n=k+1时,(cosx+isinx)k+1=(cosx+isinx)k(cosx+sinx)
=(coskx+isinkx)(cosx+isinx)=coskxcosx-sinkxsinx+(coskxsinx+sinkxcosx)i
=cos[(k+1)x]+isin[(k+1)x],
∴当n=k+1时,等式成立.
由①②得,(cosx+isinx)n=cosnx+isinnx.
点评 本题考查了数学归纳法和三角函数的两角和差的正弦余弦公式,属于中档题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
16.把病人送到医院看病的过程用框图表示,则此框图称为( )
| A. | 工序流程图 | B. | 程序流程图 | C. | 组织流程图 | D. | 程序步骤图 |
10.已知点P(tanα,cosα)在第三象限,则角α的终边在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,O坐标原点,以OF直径的圆与双曲线的一条渐近线相交于O,A两点,且|OA|=2|AF|,则双曲线的离心率等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
14.下列框图中是流程图的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
15.已知定义在(0,+∞)上的单调函数f(x),对?x∈(0,+∞),都有f[f(x)-log2x]=3,则方程f(x)-f′(x)=2的解所在的区间是( )
| A. | (0,$\frac{1}{2}$) | B. | (1,2) | C. | ($\frac{1}{2}$,1) | D. | (2,3) |
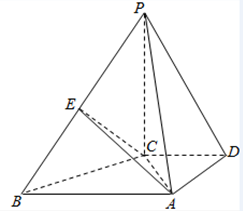 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点. 如图在三棱柱ABC-A1B1C1中,侧面AA1C1C是矩形,且侧面AA1C1C⊥底面AA1B1B,M是AB的中点,若AA1=2,AC=1,∠A1AB=60°,CB1⊥A1B.
如图在三棱柱ABC-A1B1C1中,侧面AA1C1C是矩形,且侧面AA1C1C⊥底面AA1B1B,M是AB的中点,若AA1=2,AC=1,∠A1AB=60°,CB1⊥A1B.