题目内容
4.设θ为第二象限角,若$tan({θ+\frac{π}{4}})=\frac{1}{3}$,则tanθ=-$\frac{1}{2}$;sinθ+cosθ=-$\frac{\sqrt{5}}{5}$.分析 先根据两角和差的正切公式,求出tanθ=-$\frac{1}{2}$,继而得到2sinθ=-cosθ,再根据sin2θ+cos2θ=1,求出sinθ=$\frac{\sqrt{5}}{5}$,cosθ=-$\frac{2\sqrt{5}}{5}$,问题得以解决.
解答 解:tan(θ+$\frac{π}{4}$)=$\frac{tanθ+tan\frac{π}{4}}{1-tanθtan\frac{π}{4}}$=$\frac{1+tanθ}{1-tanθ}$=$\frac{1}{3}$,
解得tanθ=-$\frac{1}{2}$,
∴tanθ=$\frac{sinθ}{cosθ}$=-$\frac{1}{2}$,
∴2sinθ=-cosθ,
∵sin2θ+cos2θ=5sin2θ=1,θ为第二象限角
∴sinθ=$\frac{\sqrt{5}}{5}$,cosθ=-$\frac{2\sqrt{5}}{5}$,
∴sinθ+cosθ=-$\frac{\sqrt{5}}{5}$.
故答案为:-$\frac{1}{2}$,-$\frac{\sqrt{5}}{5}$.
点评 本题考查了两角和差的正切公式,正弦和余弦的关系,属于基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
16.把病人送到医院看病的过程用框图表示,则此框图称为( )
| A. | 工序流程图 | B. | 程序流程图 | C. | 组织流程图 | D. | 程序步骤图 |
14.下列框图中是流程图的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
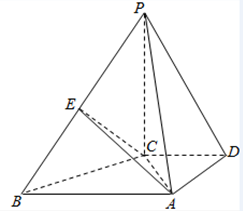 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.