题目内容
3.已知从某飞船带回的某种植物种子每粒成功发芽的概率都为$\frac{1}{3}$,某植物研究所进行该种子的发芽试验,每次试验种一粒种子,每次试验结果相互独立.假定某次试验种子发芽则称该次试验是成功的,如果种子没有发芽,则称该次试验是失败的.若该研究所共进行四次试验,设ξ表示四次试验结束时试验成功的次数与失败的次数之差的绝对值.(1)求ξ=2的概率;
(2)求ξ≥2的概率.
分析 (1)由题意知ξ的可能取值为0,2,4,“ξ=2”指的是试验成功3次,失败1次; 或试验成功1次,失败3次.再根据n次独立重复试验中恰好发生k次的概率公式求得P(ξ=2)的值.
(2)“ξ=0”指的是试验成功2次,失败2次,根据 P(ξ≥2)=1-P(ξ=0),求得结果.
解答 解:(1)由题意知ξ的可能取值为0,2,4,
“ξ=2”指的是试验成功3次,失败1次; 或试验成功1次,失败3次.
∴P(ξ=2)=${C}_{4}^{3}$•${(\frac{1}{3})}^{3}$•$\frac{2}{3}$+${C}_{4}^{1}$•$\frac{1}{3}$•${(\frac{2}{3})}^{3}$=$\frac{8}{81}$+$\frac{32}{81}$=$\frac{40}{81}$.
(2)∵“ξ=0”指的是试验成功2次,失败2次.
∴P(ξ≥2)=1-P(ξ=0)=1-$\frac{24}{81}$=$\frac{19}{27}$.
点评 本题考查相互独立事件的概率乘法公式及n次独立重复试验中恰好发生k次的概率公式,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
14.下列框图中是流程图的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
15.已知定义在(0,+∞)上的单调函数f(x),对?x∈(0,+∞),都有f[f(x)-log2x]=3,则方程f(x)-f′(x)=2的解所在的区间是( )
| A. | (0,$\frac{1}{2}$) | B. | (1,2) | C. | ($\frac{1}{2}$,1) | D. | (2,3) |
13.在密码学中,直接可以看到内容的为明码,对明码进行某种处理后得到的内容为密码.有一种密码将英文的26个字母a,b,c,…,z(不分大小写)依次对应1,2,3,…,26这26个自然数,见表:
给出明码对应的序号x和密码对应的序号y的变换公式:y=$\left\{\begin{array}{l}\frac{x+1}{2},x为奇数,且1≤x≤26\\ \frac{x}{2}+13,x为偶数,且1≤x≤26\end{array}$
利用它可以将明码转换成密码,如5→$\frac{5+1}{2}$=3,即e变成c,8→$\frac{8}{2}$+13=17,即h变成q.按上述公式,若将某明码译成的密码是shxc,那么原来的明码是love.
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
利用它可以将明码转换成密码,如5→$\frac{5+1}{2}$=3,即e变成c,8→$\frac{8}{2}$+13=17,即h变成q.按上述公式,若将某明码译成的密码是shxc,那么原来的明码是love.
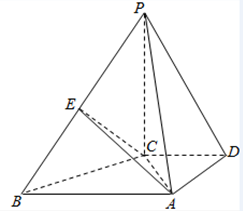 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.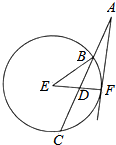 如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.
如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.