题目内容
2.设数列{an},{bn}满足a1=b1=6,a2=b2=4,且数列{an-$\frac{n^2}{2}$}(n∈N*)是等差数列,数列{bn-2}(n∈N*)是等比数列.(1)求数列{an}和{bn}的通项公式;
(2)是否存在k∈N+,使ak-bk∈(0,$\frac{1}{2}$),若存在,求出k,若不存在,说明理由.
分析 (1)根据{bn-2}(n∈Z)是等比数列,可求{bn-2}的通项公式,进而可求数列{bn}的通项公式;根据数列{an-$\frac{n^2}{2}$},结合等差数列的性质即可求{an}的通项公式;
(2)设f(k)=ak-bk,求出函数f(k)的表达式,进而可求其范围,从而得结论.
解答 解:(1)∵{bn-2} (n∈Z+)为等比数列,又b1-2=4,b2-2=2,
∴公比$q=\frac{1}{2}$,${b_n}-2=4•{({\frac{1}{2}})^{n-1}}$,即${b_n}=2+4•{({\frac{1}{2}})^{n-1}}$(n∈N+),
∵{an-$\frac{n^2}{2}$}(n∈N*)是等差数列,又a1-$\frac{1}{2}$=$6-\frac{1}{2}=\frac{11}{2}$,a2-$\frac{4}{2}$=2,
∴公差d=2-$\frac{11}{2}$=-$\frac{7}{2}$,
则an-$\frac{n^2}{2}$=$\frac{11}{2}$-$\frac{7}{2}$(n-1)=-$\frac{7}{2}$n+9,
即an=$\frac{n^2}{2}$-$\frac{7}{2}$n+9=$\frac{{n}^{2}-7n+18}{2}$.
(3)设f(k)=ak-bk=($\frac{1}{2}{k}^{2}-\frac{7}{2}k+9$)-[2+4($\frac{1}{2}$)n-1]
=$\frac{1}{2}$[(k-$\frac{7}{2}$)2-$\frac{49}{4}$]-4($\frac{1}{2}$)n-1+7,
则当k≥4时,f(k)是增函数.
又∵f(4)=$\frac{1}{2}$,
∴当k≥2时,f(k)≥$\frac{1}{2}$,
又∵f(1)=f(2)=f(3)=0,
所以不存在k,使ak-bk∈(0,$\frac{1}{2}$).
点评 本题的考点是等差数列的通项公式,主要考查数列通项的求解,考查是否存在性问题,关键是转化为等差数列、等比数列研究问题.综合性较强,难度较大.

| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
| A. |  | B. |  | ||
| C. |  | D. |  |
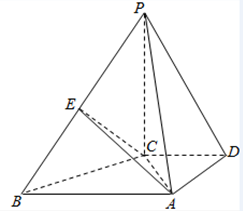 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.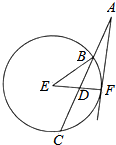 如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.
如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=$\frac{1}{3}$AC,作直线AF与圆E相切于点F,连接EF交BC于点D,己知圆E的半径为2,∠EBC=$\frac{π}{6}$.