题目内容
1.在△ABC中,已知b=3$\sqrt{2}$,c=3$\sqrt{3}$,B=45°,求A,C和a.分析 首先由正弦定理求得sinC=$\frac{\sqrt{3}}{2}$,得到角C的大小,然后由三角形内角和定理求得A,再由正弦定理求得a.
解答 解:在△ABC中,∵b=3$\sqrt{2}$,c=3$\sqrt{3}$,B=45°,
由正弦定理可得:$\frac{b}{sinB}=\frac{c}{sinC}$,即$\frac{3\sqrt{2}}{sin45°}=\frac{3\sqrt{3}}{sinC}$,
∴sinC=$\frac{\sqrt{3}}{2}$,
∵0°<C<135°,∴C=60°或C=120°.
当C=60°时,A=75°,
则由$\frac{a}{sinA}=\frac{b}{sinB}$,得$\frac{a}{sin75°}=\frac{3\sqrt{2}}{sin45°}$,∴a=$\frac{3(\sqrt{6}+\sqrt{2})}{2}$;
当C=120°时,A=15°,
则由$\frac{a}{sinA}=\frac{b}{sinB}$,得$\frac{a}{sin15°}=\frac{3\sqrt{2}}{sin45°}$,∴a=$\frac{3(\sqrt{6}-\sqrt{2})}{2}$.
点评 本题考查正弦定理在解三角形中的应用,利用正弦定理求解已知两边及一边的对角的问题时,要注意解的讨论,关键是注意大边对大角,是中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
16.把病人送到医院看病的过程用框图表示,则此框图称为( )
| A. | 工序流程图 | B. | 程序流程图 | C. | 组织流程图 | D. | 程序步骤图 |
10.已知点P(tanα,cosα)在第三象限,则角α的终边在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |

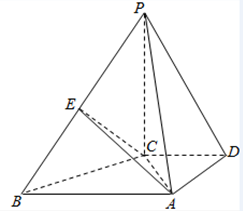 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.