题目内容
8.函数f(x)=ax2+x+$\frac{1}{2}$有两个零点,则a的取值范围为(-∞,$\frac{1}{2}$).分析 由题意得方程f(x)=0有两个不相等的实数根,即a≠0,△>0,解出不等式即可得到a的范围.
解答 解:∵函数f(x)=ax2+x+$\frac{1}{2}$有两个零点,显然a≠0
即函数f(x)=ax2+x+$\frac{1}{2}$的图象与x轴有两个交点
则△>0
∴1-4×a×$\frac{1}{2}$=1-2a>0
解得a<$\frac{1}{2}$
故答案为:(-∞,$\frac{1}{2}$).
点评 本题考查函数与方程的关系,考查运算能力,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
16.把病人送到医院看病的过程用框图表示,则此框图称为( )
| A. | 工序流程图 | B. | 程序流程图 | C. | 组织流程图 | D. | 程序步骤图 |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,O坐标原点,以OF直径的圆与双曲线的一条渐近线相交于O,A两点,且|OA|=2|AF|,则双曲线的离心率等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
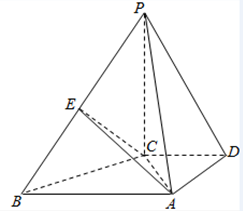 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点. 如图在三棱柱ABC-A1B1C1中,侧面AA1C1C是矩形,且侧面AA1C1C⊥底面AA1B1B,M是AB的中点,若AA1=2,AC=1,∠A1AB=60°,CB1⊥A1B.
如图在三棱柱ABC-A1B1C1中,侧面AA1C1C是矩形,且侧面AA1C1C⊥底面AA1B1B,M是AB的中点,若AA1=2,AC=1,∠A1AB=60°,CB1⊥A1B.