题目内容
17.已知实数x,y满足条件$\left\{\begin{array}{l}2x+y≥4\\ x-y≥1\\ x-2y≤2\end{array}\right.$,则z=x+2y的最小值为( )| A. | $\frac{4}{3}$ | B. | 4 | C. | 2 | D. | 3 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}2x+y≥4\\ x-y≥1\\ x-2y≤2\end{array}\right.$写出可行域如图,
化z=x+2y为y=$-\frac{x}{2}+\frac{z}{2}$,由图可知,当直线y=$-\frac{x}{2}+\frac{z}{2}$过A(2,0)时,直线在y轴上的截距最小,z有最小值等于z=2+2×0=2.
故选:C.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知复数z=(1-i)(1+2i),其中i为虚数单位,则$\overline{z}$的虚部为( )
| A. | -i | B. | 1 | C. | -1 | D. | i |
12.某天连续有7节课,其中语文、英语、物理、化学、生物5科各1节,数学2节.在排课时,要求生物课不排第1节,数学课要相邻,英语课与数学课不相邻,则不同排法的种数是( )
| A. | 408 | B. | 480 | C. | 552 | D. | 816 |
2.已知i是虚数单位,则i3+$\frac{1}{i}$=( )
| A. | -2i | B. | 2i | C. | -i | D. | i |
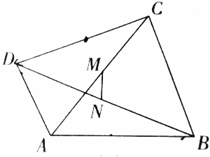 如图,四边形ABCD的对角线AC、BD的中点分别为M、N,求证:$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$(AB+CD).
如图,四边形ABCD的对角线AC、BD的中点分别为M、N,求证:$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$(AB+CD).