题目内容
18.已知在△ABC中,角A、B、C的对边分别为a、b、c,且$\frac{2}{sinB}$=$\frac{1}{sinA}$+$\frac{1}{sinC}$.(1)求角B的范围;
(2)求f(B)=2$\sqrt{3}$cos2$\frac{B}{2}$+2sin$\frac{B}{2}$cos$\frac{B}{2}$-3的最值.
分析 (1)根据正弦定理的推论,结合已知可得b=$\frac{2ac}{a+c}$,结合基本不等式和余弦定理,可得cosB$≥\frac{1}{2}$,进而得到角B的范围;
(2)利用倍角公式和辅助角公式化简函数的解析式,根据(1)中B角的范围,结合正弦型函数的图象和性质,可得答案.
解答 解:(1)∵$\frac{2}{sinB}$=$\frac{1}{sinA}$+$\frac{1}{sinC}$.
∴2sinAsinC=sinBsinC+sinAsinB,
∴2ac=bc+ab,
∴b=$\frac{2ac}{a+c}$,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}}{2ac}$-$\frac{(\frac{2ac}{a+c})^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}}{2ac}$-$\frac{2ac}{(a+c)^{2}}$,
∵a2+c2≥2ac,(a+c)2≥4ac
∴$\frac{{a}^{2}+{c}^{2}}{2ac}$≥1,$\frac{2ac}{(a+c)^{2}}$≤$\frac{1}{2}$
∴$\frac{{a}^{2}+{c}^{2}}{2ac}$-$\frac{2ac}{(a+c)^{2}}$$≥\frac{1}{2}$,
即cosB$≥\frac{1}{2}$,
∴B∈(0,$\frac{π}{3}$]
(2)f(B)=2$\sqrt{3}$cos2$\frac{B}{2}$+2sin$\frac{B}{2}$cos$\frac{B}{2}$-3=$\sqrt{3}$cosB+sinB+$\sqrt{3}$-3=2sin(B+$\frac{π}{3}$)+$\sqrt{3}$-3,
∵B∈(0,$\frac{π}{3}$]
∴B+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{2π}{3}$],
故当B+$\frac{π}{3}$=$\frac{π}{2}$,即B=$\frac{π}{6}$时,f(B)取最大值$\sqrt{3}$-1,
当B+$\frac{π}{3}$=$\frac{2π}{3}$,即B=$\frac{π}{3}$时,f(小)取最大值2$\sqrt{3}$-3
点评 本题考查的知识点是正弦定理,余弦定理,倍角公式,辅助角公式,正弦型函数的图象和性质,是三角函数的综合应用,难度中档.

| A. | -i | B. | 1 | C. | -1 | D. | i |
| A. | (1,+∞) | B. | ($\frac{2\sqrt{3}}{3}$,+∞) | C. | ($\frac{\sqrt{5}+1}{2}$,+∞) | D. | ($\sqrt{2}$+1,+∞) |
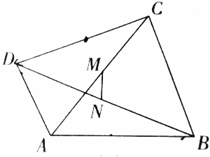 如图,四边形ABCD的对角线AC、BD的中点分别为M、N,求证:$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$(AB+CD).
如图,四边形ABCD的对角线AC、BD的中点分别为M、N,求证:$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$(AB+CD).