题目内容
已知函数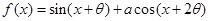 ,其中
,其中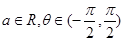
(1)当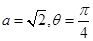 时,求
时,求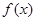 在区间
在区间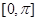 上的最大值与最小值;
上的最大值与最小值;
(2)若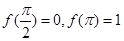 ,求
,求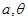 的值.
的值.
(1)最大值为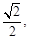 最小值为-1. (2)
最小值为-1. (2)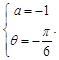
解析试题分析:(1)求三角函数最值,首先将其化为基本三角函数形式:当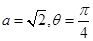 时,
时,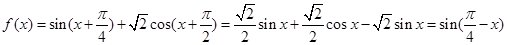 ,再结合基本三角函数性质求最值:因为
,再结合基本三角函数性质求最值:因为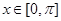 ,从而
,从而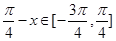 ,故
,故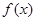 在
在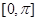 上的最大值为
上的最大值为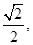 最小值为-1.(2)两个独立条件求两个未知数,联立方程组求解即可. 由
最小值为-1.(2)两个独立条件求两个未知数,联立方程组求解即可. 由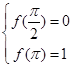 得
得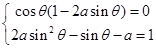 ,又
,又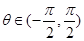 知
知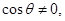 解得
解得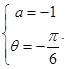
试题解析:解(1)当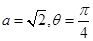 时,
时,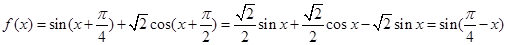
因为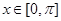 ,从而
,从而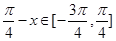
故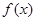 在
在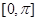 上的最大值为
上的最大值为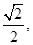 最小值为-1.
最小值为-1.
(2)由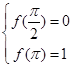 得
得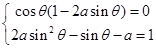 ,又
,又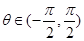 知
知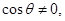 解得
解得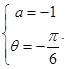
考点:三角函数性质

练习册系列答案
相关题目
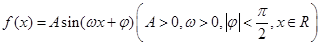 图象的一部分如图所示.
图象的一部分如图所示. 的解析式;
的解析式; 时,求函数
时,求函数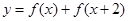 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.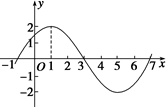
 cos
cos cos
cos .
. ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.
 时,
时, 的最小值为– 2 ,求a的值.
的最小值为– 2 ,求a的值.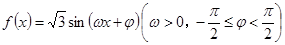 的图像关于直线
的图像关于直线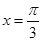 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为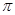 .
.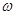 和
和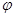 的值;
的值;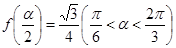 ,求
,求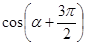 的值.
的值. .
. ,求
,求 的取值构成的集合.
的取值构成的集合. ,求
,求 的值.
的值. 图象的一部分如图所示.
图象的一部分如图所示.
 的解析式;
的解析式; 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值. )(x≠0),且cosα=
)(x≠0),且cosα=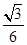 x,求sinα、tanα的值.
x,求sinα、tanα的值. x﹣
x﹣ ),x∈R.
),x∈R. ,f(3
,f(3 )=
)=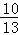 ,f(3β+
,f(3β+ )=
)= .求sin(α+β)的值.
.求sin(α+β)的值.