题目内容

函数f（x）=（lnx）2-lnx-2的单调递减区间为
 
．
考点：利用导数研究函数的单调性
专题：计算题,导数的综合应用
分析：求出函数的导数，令导数小于0，解不等式，注意x＞0，解得即可得到单调减区间．
解答： 解：f（x）=（lnx）2-lnx-2（x＞0）的导数
f′（x）=2lnx•
1
x
-
1
x
=
1
x
（2lnx-1），
令f′（x）＜0，则2lnx＜1，解得，0＜x＜
e
．
即有f（x）的单调减区间为（0，
e
）．
故答案为：（0，
e
）．
点评：本题考查导数的运用：求单调区间，注意函数的定义域，考查运算能力，属于基础题和易错题．
练习册系列答案
相关题目
与圆O：x2+y2=4外切于点P（1，-
3
），且半径为4的圆C的方程为
 
．
有下列五个命题：
①在△ABC中，p：A＞B；q：sinA＞sinB；则命题p是命题q的充要条件；
②p：数列{an}是等差数列，q：数列{an}是单调数列；命题p是命题q的充要条件；
③P：△ABC是锐角△ABC，q：sinA＞cosB；则命题p是命题q的充要条件；
④α≠
π
6
或β≠
π
6
是cos（α+β）≠
1
2
成立的必要不充分条件；
⑤a＜0是方程ax2+2x+1=0至少有一个负数根的充分不必要条件．
其中正确的命题序号是
 
．
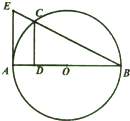如图，EA是圆O的切线，割线EB交圆O于点C，C在直径AB上的射影为D，CD=2，BD=4，则EA=
 
．
已知数列{an}的前n项和为Sn，且满足：Sn=n-an，
（1）求a1，a2，a3的值；
（2）求证：数列{an-1}是等比数列，并求{an}通项公式；
（3）令bn=（2-n）（an-1），（n=1，2，3…），如果对任意n∈N*，都有bn+
1
4
t≤t2，求实数t的取值范围．
若方程（
1
2
）x-2x=6的解所在的区间是（k，k+1），则整数k=
 
．
已知圆的直径AB=10cm，C是圆周上一点（不同于A、B点），CD⊥AB于D，CD=3cm，则BD=
 
cm．
如表是一组实验的统计数据：
x0123
y1230
（1）求线性回归方程
y
=
b
x+
a
？
（2）填写残差分布表．（表格在答题卷上）．并计算残差的均值
.
e
．
（3）求x对y的贡献率R2？并说明回归直线方程拟合效果．
（公式：
b
=
n
i=1
xiyi-n
.
x
.
y
n
i=1
xi2-n
-2
x
；R2=1-
n
i=1
(yi-
yi
)2
n
i=1
(yi-
.
y
)2
）
a
=（4，-2，-4），
b
=（6，-3，2），则（2
a
-3
b
）•（
a
+2
b
）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网