题目内容
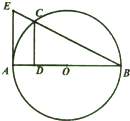如图，EA是圆O的切线，割线EB交圆O于点C，C在直径AB上的射影为D，CD=2，BD=4，则EA=考点：与圆有关的比例线段
专题：立体几何
分析：由相交弦定理，得CD2=AD•BD，由△BDC∽△BAE，得
=
，由此能求出AE．
| BD |
| BA |
| CD |
| AE |
解答：
解：由相交弦定理，得CD2=AD•BD，
即22=AD×4，
解得AD=1，∴AB=1+4=5，
∵EA是圆O的切线，C在直径AB上的射影为D，
∴△BDC∽△BAE，
∴
=
，
∴AE=
=
=
．
故答案为：
．
即22=AD×4，
解得AD=1，∴AB=1+4=5，
∵EA是圆O的切线，C在直径AB上的射影为D，
∴△BDC∽△BAE，
∴
| BD |
| BA |
| CD |
| AE |
∴AE=
| BA•CD |
| BD |
| 5×2 |
| 4 |
| 5 |
| 2 |
故答案为：
| 5 |
| 2 |
点评：本题考查与圆有关的线段长的求法，是中档题，解题时要注意相交弦定理的合理运用．
练习册系列答案
相关题目
如图，直线y=x+b与椭圆
已知等腰Rt△ABC中，∠C=90°．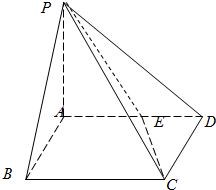
在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为正方形，且PA=AD=2，E为棱AD的中点．