题目内容
若方程(
)x-2x=6的解所在的区间是(k,k+1),则整数k= .
| 1 |
| 2 |
考点:函数的零点
专题:函数的性质及应用
分析:令f(x)=(
)x-2x-6 在区间是(k,k+1)上有唯一零点,可得f(k)f(k+1)<0,从而求得k的值.
| 1 |
| 2 |
解答:
解:令f(x)=(
)x-2x-6,根据方程(
)x-2x=6的解所在的区间是(k,k+1),f(x)在(k,k+1)上单调第减,
可得f(x)=(
)x-2x-6 在区间是(k,k+1)上有唯一零点,故有f(k)f(k+1)<0.
再根据f(-2)=2>0,f(-1)=-2<0,可得k=-2,
故答案为:-2.
| 1 |
| 2 |
| 1 |
| 2 |
可得f(x)=(
| 1 |
| 2 |
再根据f(-2)=2>0,f(-1)=-2<0,可得k=-2,
故答案为:-2.
点评:本题主要考查函数零点的判定定理的应用,函数零点和方程的根的关系,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知函数f(x)=2sin(-2x+
)+1,若x∈(-
,
),则函数f(x)的值域为( )
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
A、(1-
| ||||
B、(1-
| ||||
C、[-1,1+
| ||||
| D、[-1,3] |
 如图,OMN是半径为2,圆心角为120°的扇形,ABCD是扇形的内接矩形.
如图,OMN是半径为2,圆心角为120°的扇形,ABCD是扇形的内接矩形.
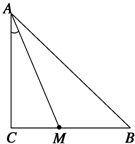 已知等腰Rt△ABC中,∠C=90°.
已知等腰Rt△ABC中,∠C=90°.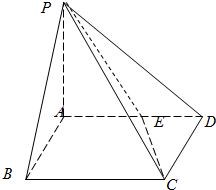 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E为棱AD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E为棱AD的中点.