��Ŀ����
������������⣺
���ڡ�ABC�У�p��A��B��q��sinA��sinB��������p������q�ij�Ҫ������
��p������{an}�ǵȲ����У�q������{an}�ǵ������У�����p������q�ij�Ҫ������
��P����ABC����ǡ�ABC��q��sinA��cosB��������p������q�ij�Ҫ������
�ܦ���
��¡�
��cos����+�£���
�����ı�Ҫ�����������
��a��0�Ƿ���ax2+2x+1=0������һ���������ij�ֲ���Ҫ������
������ȷ����������� ��
���ڡ�ABC�У�p��A��B��q��sinA��sinB��������p������q�ij�Ҫ������
��p������{an}�ǵȲ����У�q������{an}�ǵ������У�����p������q�ij�Ҫ������
��P����ABC����ǡ�ABC��q��sinA��cosB��������p������q�ij�Ҫ������
�ܦ���
| �� |
| 6 |
| �� |
| 6 |
| 1 |
| 2 |
��a��0�Ƿ���ax2+2x+1=0������һ���������ij�ֲ���Ҫ������
������ȷ�����������
���㣺���������ж���Ӧ��
ר�⣺������
���������ڡ�ABC�У������Ҷ����ɵ�
=
������q��sinA��sinB?a��b?A��B�������жϳ���
��p������{an}�ǵȲ����У�ȡan=1�������ǵ������У�q������{an}�ǵ������У�ȡan=
�������ǵȲ����У������жϳ���
�۶���q��sinA��cosB=sin(
-B)���ɢٿɵ�A��
-B����֪��ABC���Բ�����ǡ�ABC�������жϳ���
����cos����+�£���
�������ɵæ���
��¡�
������֮������������ȡ��+��=2��+
�������жϳ���
�ݷ���ax2+2x+1=0��ʵ�����������0��a=0�����a��1��a=0����a��0ʱ�����̵�����ʵ��������x1x2=
����a��0�Ƿ���ax2+2x+1=0������һ������������a=0�����̵�ʵ����Ϊ-
�������жϳ���
| a |
| sinA |
| b |
| sinB |
��p������{an}�ǵȲ����У�ȡan=1�������ǵ������У�q������{an}�ǵ������У�ȡan=
| 1 |
| n |
�۶���q��sinA��cosB=sin(
| �� |
| 2 |
| �� |
| 2 |
����cos����+�£���
| 1 |
| 2 |
| �� |
| 6 |
| �� |
| 6 |
| �� |
| 3 |
�ݷ���ax2+2x+1=0��ʵ�����������0��a=0�����a��1��a=0����a��0ʱ�����̵�����ʵ��������x1x2=
| 1 |
| a |
| 1 |
| 2 |
���
�⣺���ڡ�ABC�У������Ҷ����ɵ�
=
������q��sinA��sinB?a��b?A��B���������p������q�ij�Ҫ��������ȷ��
��p������{an}�ǵȲ����У�ȡan=1�������ǵ������У���p�Ʋ���q��q������{an}�ǵ������У�ȡan=
�������ǵȲ����У��������p������q�ļȲ����Ҳ����Ҫ��������˲���ȷ��
�۶���q��sinA��cosB=sin(
-B)���ɢٿɵ�A��
-B����ˡ�ABC���Բ�����ǡ�ABC���������p������q�ij�Ҫ��������ȷ��
����cos����+�£���
�������ɵæ���
��¡�
������֮������������ȡ��+��=2��+
����˦���
��¡�
��cos����+�£���
�����ı�Ҫ�����������
�ݷ���ax2+2x+1=0��ʵ�����������0��a=0�����a��1��a=0����a��0ʱ�����̵�����ʵ��������x1x2=
�����a��0�Ƿ���ax2+2x+1=0������һ���������ij��������
��a=0�����̵�ʵ����Ϊ-
����a��0�Ƿ���ax2+2x+1=0������һ���������ij�ֲ���Ҫ��������ȷ��
������ȷ����������� �٢ܢݣ�
�ʴ�Ϊ���٢ܢݣ�
| a |
| sinA |
| b |
| sinB |
��p������{an}�ǵȲ����У�ȡan=1�������ǵ������У���p�Ʋ���q��q������{an}�ǵ������У�ȡan=
| 1 |
| n |
�۶���q��sinA��cosB=sin(
| �� |
| 2 |
| �� |
| 2 |
����cos����+�£���
| 1 |
| 2 |
| �� |
| 6 |
| �� |
| 6 |
| �� |
| 3 |
| �� |
| 6 |
| �� |
| 6 |
| 1 |
| 2 |
�ݷ���ax2+2x+1=0��ʵ�����������0��a=0�����a��1��a=0����a��0ʱ�����̵�����ʵ��������x1x2=
| 1 |
| a |
��a=0�����̵�ʵ����Ϊ-
| 1 |
| 2 |
������ȷ����������� �٢ܢݣ�
�ʴ�Ϊ���٢ܢݣ�
���������⿼���˼��������й�֪ʶ�����Ҷ�����Ӧ�á����Ǻ����ĵ����ԡ�һԪ������ʵ�������б�ʽ�Ĺ�ϵ����������������������������������⣮

��ϰ��ϵ�д�
 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
�����Ŀ
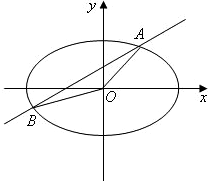 ��ͼ��ֱ��y=x+b����Բ
��ͼ��ֱ��y=x+b����Բ