题目内容
如表是一组实验的统计数据:
(1)求线性回归方程
=
x+
?
(2)填写残差分布表.(表格在答题卷上).并计算残差的均值
.
(3)求x对y的贡献率R2?并说明回归直线方程拟合效果.
(公式:
=
;R2=1-
)
| x | 0 | 1 | 2 | 3 |
| y | 1 | 2 | 3 | 0 |
 |
| y |
 |
| b |
 |
| a |
(2)填写残差分布表.(表格在答题卷上).并计算残差的均值
. |
| e |
(3)求x对y的贡献率R2?并说明回归直线方程拟合效果.
(公式:
 |
| b |
| |||||||
|
| |||||
|
考点:线性回归方程
专题:计算题,概率与统计
分析:(1)利用公式求出b,a,即可求线性回归方程
=
x+
?
(2)利用所给数据填写残差分布表,并计算残差的均值
.
(3)R2=1-
=0.04.说明回归直线方程拟合效果较差
 |
| y |
 |
| b |
 |
| a |
(2)利用所给数据填写残差分布表,并计算残差的均值
. |
| e |
(3)R2=1-
| 4.8 |
| 5 |
解答:
解:(1)由
得b=
=-0.2;a=
+0.2×
=1.8
线性回归方程y=-0.2x+1.8(6分)
(2)残差分布表为:
残差的均值为0(10分)
(3)
(yi-
i)2=(-0.8)2+0.42+1.62+(-1.2)2=4.8,
(yi-
)2=(-0.5)2+0.52+1.52+(-1.5)2=5
∴R2=1-
=0.04.
说明回归直线方程拟合效果较差.(14分)
| 数据编号i | 1 | 2 | 3 | 4 | 合计 |
| xi | 0 | 1 | 2 | 3 | 6 |
| yi | 1 | 2 | 3 | 0 | 6 |
| xi2 | 0 | 1 | 4 | 9 | 14 |
| xiyi | 0 | 2 | 6 | 0 | 8 |
8-4×
| ||||
14-4×(
|
| 3 |
| 2 |
| 3 |
| 2 |
线性回归方程y=-0.2x+1.8(6分)
(2)残差分布表为:
| 数据编号i | 1 | 2 | 3 | 4 | ||
| xi | 0 | 1 | 2 | 3 | ||
| yi | 1 | 2 | 3 | 0 | ||
| 1.8 | 1.6 | 1.4 | 1.2 | ||
| -0.8 | 0.4 | 1.6 | -1.2 |
(3)
| 4 |
 |
| i=1 |
 |
| y |
| 4 |
 |
| i=1 |
. |
| yi |
∴R2=1-
| 4.8 |
| 5 |
说明回归直线方程拟合效果较差.(14分)
点评:本题考查线性回归方程、残差分布表,考查回归直线方程拟合效果,考查学生的计算能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
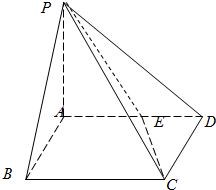 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E为棱AD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E为棱AD的中点.