题目内容
17. 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.(Ⅰ)求证:平面PAD⊥平面PBD;
(Ⅱ)若PD=AD=1,$\overrightarrow{PE}$=2$\overrightarrow{EB}$,求二面角P-AD-E的余弦值.
分析 (Ⅰ)根据面面垂直的判定定理即可证明平面PBD⊥平面PAD;
(Ⅱ)以D为原点,DA所在直线为x轴,DB所在直线为y轴建立直角坐标系,求出平面的法向量,利用向量的夹角公式,即可求出二面角的平面角.
解答 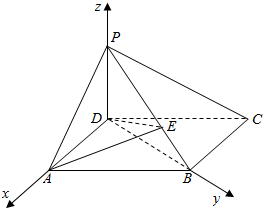 (Ⅰ)证明:∵PD⊥底面ABCD,BD?底面ABCD,
(Ⅰ)证明:∵PD⊥底面ABCD,BD?底面ABCD,
∴PD⊥BD…(2分)
∵∠ADB=90°,∴AD⊥BD…(3分)
∵AD∩PD=D
∴BD⊥平面PAD…(5分)
∵BD?平面PBD,
∴平面PAD⊥平面PBD…(7分)
(Ⅱ)解:以D为原点,DA所在直线为x轴,DB所在直线为y轴建立直角坐标系
D(0,0,0),P(0,0,1),A(1,0,0),B(0,$\sqrt{3}$,0),
设P(0,x,y),∵$\overrightarrow{PE}=2\overrightarrow{EB}$,∴$E(0,\frac{{2\sqrt{3}}}{3},\frac{1}{3})$…(9分)
∵BD⊥平面PAD,∴平面PAD的一个法向量$\overrightarrow{n_1}=(0,1,0)$…(10分)
设平面ADE的一个法向量$\overrightarrow{n_2}=(x,y,z)$,
$\left\{\begin{array}{l}\overrightarrow{n_2}•\overrightarrow{DE}=0\\ \overrightarrow{n_2}•\overrightarrow{DA}=0\end{array}\right.$,$\left\{\begin{array}{l}\frac{{2\sqrt{3}}}{3}y+\frac{1}{3}z=0\\ x=0\end{array}\right.$,∴$x=0,y=1,z=-2\sqrt{3}$
解得$\overrightarrow{n_2}=(0,1,-2\sqrt{3})$…(13分)
设α为所求的角,cosα=$\frac{1}{1×\sqrt{13}}$=$\frac{\sqrt{13}}{13}$…(15分)
点评 本题主要考查空间面面垂直的判定以及空间二面角的求解,利用向量法进行求解是解决空间二面角的常用方法

 将正整数按如图排列,其中处于从左到右第m列从下到上第n行的数
将正整数按如图排列,其中处于从左到右第m列从下到上第n行的数记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(10,3)
=69;A(1,n)=$\frac{n(n+1)}{2}$.
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
| 积极参加班级工作 | 不积极参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性不高 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(Ⅱ)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(Ⅲ)学生的积极性与对待班级工作的态度是否有关系?请说明理由.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 如图,C是圆O的直径AB上一点,CD⊥AB,与圆O相交于点D,与弦AF交于点E,与BF的延长线相交于点G.GT与圆相切于点T.
如图,C是圆O的直径AB上一点,CD⊥AB,与圆O相交于点D,与弦AF交于点E,与BF的延长线相交于点G.GT与圆相切于点T.