题目内容
12.已知函数f(x)=|x+a|+|x+$\frac{1}{a}$|(a>0)(Ⅰ)当a=2时,求不等式f(x)>3的解集;
(Ⅱ)证明:$f(m)+f(-\frac{1}{m})≥4$.
分析 (Ⅰ)当a=2时,求不等式即|x+2|+|x+$\frac{1}{2}$|>3,再利用对值的意义求得它的解集.
(Ⅱ)由条件利用绝对值三角不等式、基本不等式,证得要证的结论.
解答 解:(Ⅰ)当a=2时,求不等式f(x)>3,即|x+2|+|x+$\frac{1}{2}$|>3.
而|x+2|+|x+$\frac{1}{2}$|表示数轴上的x对应点到-2、-$\frac{1}{2}$对应点的距离之和,
而0和-3对应点到-$\frac{11}{4}$、$\frac{1}{4}$对应点的距离之和正好等于3,
故不等式f(x)>3的解集为{x|x<-$\frac{11}{4}$,或 x>$\frac{1}{4}$}.
(Ⅱ)证明:∵f(m)+f(-$\frac{1}{m}$)=|m+a|+|m+$\frac{1}{a}$|+|-$\frac{1}{m}$+a||-$\frac{1}{m}$+$\frac{1}{a}$|
=(|m+a|+|-$\frac{1}{m}$+a|)+(|m+$\frac{1}{a}$|+|-$\frac{1}{m}$+$\frac{1}{a}$|)≥2(|m+$\frac{1}{m}$|)=2(|m|+|$\frac{1}{m}$|)≥4,
∴要证得结论成立.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,绝对值三角不等式、基本不等式的应用,属于中档题.

练习册系列答案
相关题目
3.命题p:已知α⊥β,则?l?α,都有l⊥β;命题q:已知l∥α,则?m?α,使得l不平行于m(其中α、β是平面,l、m是直线),则下列命题中真命题的是( )
| A. | (¬p)∧(¬q) | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
7.某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
(Ⅰ)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(Ⅱ)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(Ⅲ)学生的积极性与对待班级工作的态度是否有关系?请说明理由.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 积极参加班级工作 | 不积极参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性不高 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(Ⅱ)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(Ⅲ)学生的积极性与对待班级工作的态度是否有关系?请说明理由.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
17.已知全集U=R,集合A={y|y=2x,x∈R},B={x|x≥2},则下图中阴影部分所表示的集合为( )
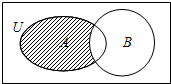

| A. | ∅ | B. | {0,1} | C. | (0,2) | D. | (-∞,2) |
1.在等比数列{an}中,a1=2,且a3+a5=40,则{an}的公比q=( )
| A. | ±5 | B. | ±4 | C. | $±\sqrt{5}$ | D. | ±2 |