题目内容
18．已知函数f（x）=-1+5（x-1）-C${\;}_{5}^{2}$（x-1）2+C${\;}_{5}^{3}$（x-1）3-5（x-1）4+（x-1）5，若f（a）=32，则实数a的值为4．分析 利用二项式定理化简函数，再利用f（a）=32，求实数a的值．
解答 解：f（x）=-1+5（x-1）-C${\;}_{5}^{2}$（x-1）2+C${\;}_{5}^{3}$（x-1）3-5（x-1）4+（x-1）5=（-1+x-1）5=（x-2）5，
因为f（a）=32，
所以（a-2）5=32，
所以a=4．
故答案为：4．
点评 本题考查二项式定理，考查学生的计算能力，正确化简函数是关键．
练习册系列答案
相关题目
9．已知随机变量ξ的分布列是
其中$α∈（{0，\frac{π}{2}}）$，则Eξ=（ ）
| ξ | -1 | 0 | 2 |
| P | $\frac{sinα}{4}$ | $\frac{sinα}{4}$ | cosα |
| A． | $2cosα-\frac{1}{4}sinα$ | B． | $cosα+\frac{1}{2}sinα$ | C． | 0 | D． | 1 |
6．“序数”指每个数字比其左边的数字大的自然数（如1246），在两位的“序数”中任取一个数比36大的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{5}$ |
10．己知集合A={x|x2-2x＞0}，B={x||x|＜$\sqrt{5}$}，则（ ）
| A． | A∪B=R | B． | A∩B=∅ | C． | A?B | D． | A⊆B |
如图，矩形ABCD中，AB=2，BC=4，以矩形ABCD的中心为原点，过矩形ABCD的中心平行于BC的直线为x轴，建立直角坐标系，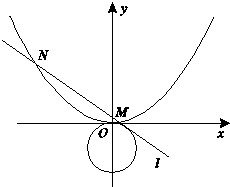
已知抛物线的顶点在坐标原点，焦点在y轴上，且过点（2，1）．