题目内容
20.点M(x,y)的函数y=-2x+8的图象上,当x∈[2,3]时,求:(1)$\frac{y}{x}$的最大值和最小值;
(2)$\frac{y+1}{x+1}$的取值范围.
分析 考查直线段的图形,利用(1)$\frac{y}{x}$的几何意义求解最大值和最小值;
(2)通过$\frac{y+1}{x+1}$的几何意义求解取值范围即可.
解答  解:如图:
解:如图:
(1)$\frac{y}{x}$的几何意义是线段上的点与坐标原点连线的斜率,
由图象可知,$\frac{y}{x}$的最大值为:KOA=2,
$\frac{y}{x}$的最小值为:KOB=$\frac{2}{3}$;
(2)$\frac{y+1}{x+1}$的几何意义是图象中,线段上的点与(-1,-1)连线的斜率,最大值为KCA=$\frac{4+1}{2+1}$=$\frac{5}{3}$,最小值为:KCB=$\frac{2+1}{3+1}$=$\frac{3}{4}$;
$\frac{y+1}{x+1}$的取值范围:[$\frac{3}{4},\frac{5}{3}$].
点评 本题考查直线的斜率,线性规划的应用,考查数形结合以及计算能力.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
10.已知全集U=R,集合A={x∈R|-2≤2x≤1},集合B={x∈R||x|<1},则CU(A∩B)=( )
| A. | (-∞,-1]∪($\frac{1}{2}$,+∞) | B. | (-1,$\frac{1}{2}$] | C. | (-∞,-1)∪[-$\frac{1}{2}$,+∞) | D. | (-1,-$\frac{1}{2}$) |
11.已知函数f(x)=(2x-$\frac{1}{{2}^{x}}$)x,则下列结论中正确的是( )
| A. | 若-3≤m<n,则f(m)<f(n) | B. | 若m<n≤0,则f(m)<f(n) | ||
| C. | 若f(m)<f(n),则m2<n2 | D. | 若f(m)<f(n),则m3<n3 |
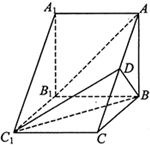 在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面A1B1C1,D为AC 的中点,A1B1=BB1=2,A1C1=BC1,∠A1C1B=60°.
在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面A1B1C1,D为AC 的中点,A1B1=BB1=2,A1C1=BC1,∠A1C1B=60°.