Question

【题目】（本小题满分分）

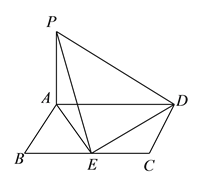
如图，平行四边形中， ， ， ， 平面， ，点为中点，连结、．

（Ⅰ）若， ，求证：平面平面．

（Ⅱ）若，试探究在直线上有几个点，使得，并说明理由．

Answer 1

【答案】详见解析

【解析】试题分析：（1）要证明平面平面，即证明平面，进而转证线线垂直即可；（2）假设边上存在使得，则连结，必有，故问题转化为：在边上是否存在点，使得．由平面几何知识，问题又可转化为：以为直径的圆与有几个交点．

试题解析：

（）证明：当， 时，

∵是平行四边形， ， ， ， 是中点，

∴， ， ，

∴，

∴．

又∵平面， 平面，

∴．

∵，

∴平面．

又∵平面，

∴平面平面．

（）假设边上存在使得，则连结，必有，故问题转化为：在边上是否存在点，使得．由平面几何知识，问题又可转化为：以为直径的圆与有几个交点．

∵， ，∴以为直径的圆圆心到直线的距离，半径为．

易知当时，以为直径的圆与无交点，

当时，以为直径的圆与有且只有一个交点，

当时，以为直径的圆与有个交点．

故当时，直线上不存在点，使得．

当时，直线上存在一个点，使得．

当时，直线上存在个点，使得．