题目内容
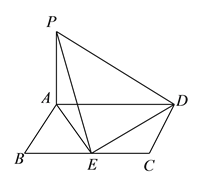
【题目】如图,四边形![]() 为矩形,
为矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,且点
,且点![]() 在
在![]() 上.
上.

(![]() )求证:
)求证:![]() ;
;
(![]() )求三棱锥
)求三棱锥![]() 的体积;
的体积;
(![]() )设点
)设点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,试在线段
,试在线段![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() .
.
【答案】(1)证明见解析;(2)![]() ;(3)当点
;(3)当点![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的一个三等分.
的一个三等分.
【解析】试题分析:(1)先证明![]() 平面
平面![]() ,得
,得![]() ,由
,由![]() 平面
平面![]() ,得
,得![]() ,从而可得
,从而可得![]() 平面
平面![]() ,由此能证明
,由此能证明![]() ;(2)在
;(2)在![]() 中,过点
中,过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,由已知及(
,由已知及(![]() )得
)得![]() ,
,![]() ,从而可得结果;(3)过点
,从而可得结果;(3)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,推导出
,推导出![]() 平面
平面![]() ,由此能求出当点
,由此能求出当点![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的一个三等分点时,
的一个三等分点时,![]() 平面
平面![]() .
.
试题解析:(![]() )证明:由
)证明:由![]() 平面
平面![]() ,
,
及![]() 得
得![]() 平面
平面![]() ,则
,则![]() ,
,
而![]() 平面
平面![]() ,则
,则![]() ,
,
又![]() ,则
,则![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,故
,故![]() .
.
(![]() )在
)在![]() 中,过点
中,过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() .
.
由已知及(![]() )得
)得![]() ,
,![]() .
.
故![]() .
.
(![]() )在
)在![]() 中过点
中过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
在![]() 中过点
中过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
则由![]() 得
得![]() ,由平面
,由平面![]()
![]() 平面
平面![]() ,
,
则![]() 平面
平面![]() ,再由
,再由![]() ,
,![]() 得
得![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,
,
故当点![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的一个三等分点时,
的一个三等分点时,![]() 平面
平面![]() .
.
【方法点晴】本题主要考查线面垂直的判定与性质,以及线面平行的判定定理、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.求:

(1) AD边所在直线的方程;
(2) DC边所在直线的方程.
【题目】某单位需要从甲、乙![]() 人中选拔一人参加新岗位培训,特别组织了
人中选拔一人参加新岗位培训,特别组织了![]() 个专项的考试,成绩统计如下:
个专项的考试,成绩统计如下:
第一项 | 第二项 | 第三项 | 第四项 | 第五项 | |
甲的成绩 |
|
|
|
|
|
乙的成绩 |
|
|
|
|
|
(1)根据有关统计知识,回答问题:若从甲、乙![]() 人中选出
人中选出![]() 人参加新岗培训,你认为选谁合适,请说明理由;
人参加新岗培训,你认为选谁合适,请说明理由;
(2)根据有关槪率知识,解答以下问题:
从甲、乙![]() 人的成绩中各随机抽取一个,设抽到甲的成绩为
人的成绩中各随机抽取一个,设抽到甲的成绩为![]() ,抽到乙的成绩为
,抽到乙的成绩为![]() ,用
,用![]() 表示满足条件
表示满足条件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.