题目内容
【题目】已知坐标平面上点![]() 与两个定点
与两个定点![]() ,
, ![]() 的距离之比等于5.
的距离之比等于5.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段的长为8,求直线
所截得的线段的长为8,求直线![]() 的方程.
的方程.
【答案】1)![]() ;(2)
;(2)![]() ,或
,或![]() .
.
【解析】试题分析:(1)运用两点间距离公式建立方程进行化简;(2)借助直线与圆的位置关系,运用圆心距、半径、弦长之间的关系建立方程待定直线的斜率,再用直线的点斜式方程分析求解:
试题解析: (1)由题意,得![]() ,即
,即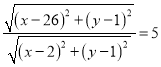 ,化简得
,化简得![]() ,即
,即![]() .
.
![]() 点
点![]() 的轨迹方程是
的轨迹方程是![]() ,轨迹是以
,轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的圆
为半径的圆
(2)当直线![]() 的斜率不存在时,
的斜率不存在时, ![]() ,此时所截得的线段的长为
,此时所截得的线段的长为![]() ,
,
![]() 符合题意,当直线
符合题意,当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() ,即
,即![]() ,圆心到
,圆心到![]() 的距离
的距离![]() ,
,
由题意,得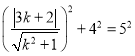 ,解得
,解得![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() .
.
即![]() .
.
综上,直线![]() 的方程为
的方程为![]() ,或
,或![]() .
.

练习册系列答案
相关题目
【题目】某单位需要从甲、乙![]() 人中选拔一人参加新岗位培训,特别组织了
人中选拔一人参加新岗位培训,特别组织了![]() 个专项的考试,成绩统计如下:
个专项的考试,成绩统计如下:
第一项 | 第二项 | 第三项 | 第四项 | 第五项 | |
甲的成绩 |
|
|
|
|
|
乙的成绩 |
|
|
|
|
|
(1)根据有关统计知识,回答问题:若从甲、乙![]() 人中选出
人中选出![]() 人参加新岗培训,你认为选谁合适,请说明理由;
人参加新岗培训,你认为选谁合适,请说明理由;
(2)根据有关槪率知识,解答以下问题:
从甲、乙![]() 人的成绩中各随机抽取一个,设抽到甲的成绩为
人的成绩中各随机抽取一个,设抽到甲的成绩为![]() ,抽到乙的成绩为
,抽到乙的成绩为![]() ,用
,用![]() 表示满足条件
表示满足条件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.