题目内容
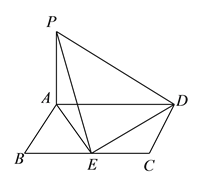
【题目】某海域的东西方向上分别有A,B两个观测点(如图),它们相距![]() 海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距
海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距![]() 海里的C点有一救援船,其航行速度为30海里/小时.
海里的C点有一救援船,其航行速度为30海里/小时.

(1)求B点到D点的距离BD;
(2)若命令C处的救援船立即前往D点营救,求该救援船到达D点需要的时间.
【答案】(1)![]() ;(2)1
;(2)1
【解析】
(1)在△DAB中利用正弦定理,求出BD;
(2)在△DCB中,利用余弦定理求出CD,根据速度求出时间.
(1)由题意知AB=5(3+![]() )海里,
)海里,
∠DBA=90°﹣60°=30°,∠DAB=90°﹣45°=45°,
∴∠ADB=180°﹣(45°+30)°=105°,
在△DAB中,由正弦定理得![]() =
=![]() ,
,
∴DB=![]() =
=![]()
=![]()
=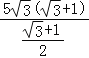 =10
=10![]() (海里)
(海里)
(2)在△DBC中,∠DBC=∠DBA+∠ABC=30°+(90°﹣60°)=60°,…(10分)
BC=20![]() (海里),由余弦定理得
(海里),由余弦定理得
CD2=BD2+BC2﹣2BDBCcos∠DBC
=300+1200﹣2×10![]() ×20
×20![]() ×
×![]() =900,
=900,
∴CD=30(海里),则需要的时间t=![]() =1(小时).
=1(小时).
答:救援船到达D点需要1小时.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案【题目】如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.求:

(1) AD边所在直线的方程;
(2) DC边所在直线的方程.
【题目】某单位需要从甲、乙![]() 人中选拔一人参加新岗位培训,特别组织了
人中选拔一人参加新岗位培训,特别组织了![]() 个专项的考试,成绩统计如下:
个专项的考试,成绩统计如下:
第一项 | 第二项 | 第三项 | 第四项 | 第五项 | |
甲的成绩 |
|
|
|
|
|
乙的成绩 |
|
|
|
|
|
(1)根据有关统计知识,回答问题:若从甲、乙![]() 人中选出
人中选出![]() 人参加新岗培训,你认为选谁合适,请说明理由;
人参加新岗培训,你认为选谁合适,请说明理由;
(2)根据有关槪率知识,解答以下问题:
从甲、乙![]() 人的成绩中各随机抽取一个,设抽到甲的成绩为
人的成绩中各随机抽取一个,设抽到甲的成绩为![]() ,抽到乙的成绩为
,抽到乙的成绩为![]() ,用
,用![]() 表示满足条件
表示满足条件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.