题目内容
(本小题满分14分)
已知动圆 经过点
经过点 ,且与圆
,且与圆 内切.
内切.
(1)求动圆圆心 的轨迹
的轨迹 的方程;(2)求轨迹E上任意一点
的方程;(2)求轨迹E上任意一点 到定点B(1,0)的距离
到定点B(1,0)的距离 的最小值,并求
的最小值,并求 取得最小值时的点M的坐标.
取得最小值时的点M的坐标.
已知动圆
 经过点
经过点 ,且与圆
,且与圆 内切.
内切.(1)求动圆圆心
 的轨迹
的轨迹 的方程;(2)求轨迹E上任意一点
的方程;(2)求轨迹E上任意一点 到定点B(1,0)的距离
到定点B(1,0)的距离 的最小值,并求
的最小值,并求 取得最小值时的点M的坐标.
取得最小值时的点M的坐标.(1)曲线 的方程为
的方程为 .
.
(2) ;
;
 的方程为
的方程为 .
.(2)
 ;
;
解:(1)依题意,动圆与定圆相内切,得| ,可知
,可知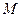 到两个定点
到两个定点 、
、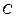 的距离的和为常数
的距离的和为常数 ,并且常数大于
,并且常数大于 ,所以点
,所以点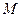 的轨迹为以A、C焦点的椭圆,可以求得
的轨迹为以A、C焦点的椭圆,可以求得 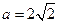 ,
, ,
, ,
,
所以曲线 的方程为
的方程为 . ……………………… 6分
. ……………………… 6分
(2)解:
 =
=
因为: ,所以,当
,所以,当 时,
时, 最小。
最小。
所以, ;
; ……………………… 14分
……………………… 14分
 ,可知
,可知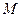 到两个定点
到两个定点 、
、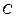 的距离的和为常数
的距离的和为常数 ,并且常数大于
,并且常数大于 ,所以点
,所以点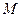 的轨迹为以A、C焦点的椭圆,可以求得
的轨迹为以A、C焦点的椭圆,可以求得 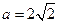 ,
, ,
, ,
,所以曲线
 的方程为
的方程为 . ……………………… 6分
. ……………………… 6分(2)解:

 =
=
因为:
 ,所以,当
,所以,当 时,
时, 最小。
最小。所以,
 ;
; ……………………… 14分
……………………… 14分
练习册系列答案
相关题目
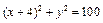 相内切,且过点A(4,0),求这个动圆圆心的轨迹方程。
相内切,且过点A(4,0),求这个动圆圆心的轨迹方程。 与
与 外切,则
外切,则 的最大值为
的最大值为 



 和圆
和圆 的位置关系是
的位置关系是
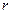 >0,两圆
>0,两圆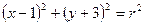 与
与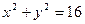 可能( )
可能( )