题目内容
圆x2+y2+8x-4y=0与圆x2+y2=20关于直线y=kx+b对称,则k与b的值分别等于( )
| A.k=-2,b=5 | B.k=2,b=5 |
| C.k=2,b=-5 | D.k=-2,b=-5 |
B
求出两圆的圆心坐标,进而求得两圆的圆心的中垂线的方程,根据直线y=kx+b即为OA的中垂线,求出k与b的值.
解:圆x2+y2+8x-4y=0即(x+4)2+(y-2)2=20,表示以A(-4,2)为圆心,以2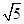 为半径的圆.
为半径的圆.
圆x2+y2=20的圆心为O(0,0),半径等于2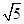 ,
,
故OA的中点为C(-2,1),OA的斜率为 ,故OA的中垂线的斜率等于2,
,故OA的中垂线的斜率等于2,
故OA的中垂线的方程为 y-1=2(x+2),即 y=2x+5.
由题意可得,直线y=kx+b即为OA的中垂线,故k与b的值分别等于2和5,
故选B.
解:圆x2+y2+8x-4y=0即(x+4)2+(y-2)2=20,表示以A(-4,2)为圆心,以2
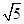 为半径的圆.
为半径的圆.圆x2+y2=20的圆心为O(0,0),半径等于2
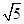 ,
,故OA的中点为C(-2,1),OA的斜率为
 ,故OA的中垂线的斜率等于2,
,故OA的中垂线的斜率等于2,故OA的中垂线的方程为 y-1=2(x+2),即 y=2x+5.
由题意可得,直线y=kx+b即为OA的中垂线,故k与b的值分别等于2和5,
故选B.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
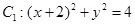 及点
及点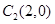 ,在圆
,在圆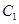 上任取一点
上任取一点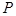 ,连接
,连接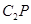 ,做线段
,做线段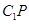 于点
于点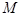 .
.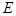 的方程;
的方程;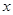 轴交于
轴交于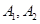 两点,在轨迹
两点,在轨迹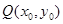
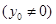 ,直线
,直线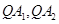 分别交
分别交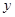 轴于
轴于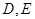 两点,求证:以线段
两点,求证:以线段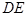 为直径的圆
为直径的圆 过两个定点,并求出定点坐标.
过两个定点,并求出定点坐标. ,0),且与定圆A´:(x-
,0),且与定圆A´:(x-
 的取值范围.
的取值范围. (
( 是正常数,
是正常数, ,
, 是参数),则圆心的轨迹是 ( )
是参数),则圆心的轨迹是 ( ) 和
和 的位置关系是( )
的位置关系是( ) 经过点
经过点 ,且与圆
,且与圆 内切.
内切. 的方程;(2)求轨迹E上任意一点
的方程;(2)求轨迹E上任意一点 到定点B(1,0)的距离
到定点B(1,0)的距离 的最小值,并求
的最小值,并求 与圆
与圆 相交,则实数
相交,则实数 的取值范围为 ▲
的取值范围为 ▲ ,
, ,则
,则 和
和 的位置关系是
的位置关系是