题目内容
已知一个动圆与圆C：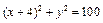
相内切，且过点A（4，0），求这个动圆圆心的轨迹方程。
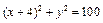相内切，且过点A（4，0），求这个动圆圆心的轨迹方程。方程是：
设动圆圆为M(x,y),半径为r,那么;
,|AC||=8
因此点M的轨迹是以A、C为焦点，长轴长为10的椭圆．
a=5,c=4,b=3,其方程是：
,|AC||=8因此点M的轨迹是以A、C为焦点，长轴长为10的椭圆．
a=5,c=4,b=3,其方程是：
练习册系列答案
相关题目
题目内容
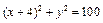相内切，且过点A（4，0），求这个动圆圆心的轨迹方程。,|AC||=8
经过点
，且与圆
内切.
的方程；（2）求轨迹E上任意一点
到定点B（1，0）的距离
的最小值，并求
与圆
相交，则实数
的取值范围为 ▲
和
相交于
两点，则直线
的方程是 。