题目内容

8．等差数列{an}的前n项和为Sn，已知am-1+am+1-am2=0，S2m-1=38，则m=（　　）
A．2B．9C．10D．19

分析 由等差数列的性质和求和公式可得m的方程，解方程可得．

解答 解：由等差数列的性质可得am-1+am+1=2am，
又∵am-1+am+1-am2=0，
∴2am-am2=0，
解得am=0或am=2，
又S2m-1=$\frac{（2m-1）（{a}_{1}+{a}_{2m-1}）}{2}$=$\frac{（2m-1）×2{a}_{m}}{2}$=（2m-1）am=38，
∴am=0应舍去，∴am=2，
∴2（2m-1）=38，解得m=10
故选：C

点评 本题考查等差数列的求和公式和性质，属基础题．

练习册系列答案
相关题目
17．已知函数f（x）=$\frac{2-x}{x+1}$．
（1）判断函数g（x）=f（x-1）+1的奇函数，并说明理由；
（2）用减函数的定义证明f（x）在（-1，0）上为减函数；
（3）求证：曲线y=ax（a为常数，且a＞1）与曲线y=f（x）有交点，且两曲线的交点不可能落在y轴的左侧．
18．已知数列{an}满足a1=32，an+1-an=n（n∈N+），则$\frac{{a}_{n}}{n}$取最小值时n=8．
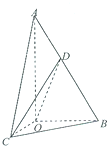16．如图，在Rt△AOB中，∠OAB=30°，斜边AB=4，Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角B-AO-C的直二面角，D是AB的中点．
（1）求证：平面COD⊥平面AOB；
（2）求异面直线AO与CD所成角的正切值．
3．已知A、B两地的距离是10km，B、C两地的距离是20km，现测得∠ABC=120°，则A、C两地的距离是10$\sqrt{7}$km．
13．求函数f（x）=$\frac{1}{3}$x3-x2-8x+1（-6≤x≤6）的单调区间、极值．
20．下列给出的输入语句、输出语句和赋值语句：则其中正确的个数是（　　）
（1）输出语句INPUT a，b，c
（2）输入语句INPUT x=3
（3）赋值语句3=A
（4）赋值语句A=B=C．
A．0B．1C．2D．3
17．cos146°+cos94°+2cos47°cos73°的值为-$\frac{1}{2}$．
18．不等式（x-1）x≥2的解集是（-∞，-1]∪[2，+∞）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网