题目内容
16.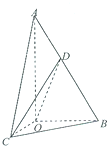 如图,在Rt△AOB中,∠OAB=30°,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C的直二面角,D是AB的中点.
如图,在Rt△AOB中,∠OAB=30°,斜边AB=4,Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C的直二面角,D是AB的中点.(1)求证:平面COD⊥平面AOB;
(2)求异面直线AO与CD所成角的正切值.
分析 (1)证明平面COD中的直线CO⊥平面AOB即可;
(2)作出异面直线AO与CD所成的角,利用直角三角形的边角关系即可
求出异面直线AO与CD所成角的正切值.
解答 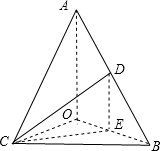 解:(1)如图所示,
解:(1)如图所示,
Rt△AOC是通过Rt△AOB以直线AO为轴旋转得到,
∴CO⊥AO,BO⊥AO;
又∵二面角B-AO-C是直二面角,
∴∠BOC是二面角B-AO-C的平面角,
即∠BOC=90°,
∴CO⊥BO;
又AO∩BO=O,
∴CO⊥平面AOB;
又∵CO?面COD,
∴平面COD⊥平面AOB;
(2)作DE⊥OB于点E,连接CE,
∴DE∥AO,
∴∠CDE是异面直线AO与CD所成的角;
在 Rt△COE中,CO=BO=$\frac{1}{2}$AB=2,OE=$\frac{1}{2}$BO=1,
∴CE=$\sqrt{{CO}^{2}{+OE}^{2}}$=$\sqrt{5}$;
又DE=$\frac{1}{2}$AO=$\sqrt{3}$,
∴tan∠CDE=$\frac{CE}{DE}$=$\frac{\sqrt{15}}{3}$,
即异面直线AO与CD所成角的正切值是$\frac{\sqrt{15}}{3}$.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了直角三角形边角关系的应用问题,是综合性题目.

练习册系列答案
相关题目
4.某程序框图如图所示,若该程序运行后输出的S的值为72,则判断框内应填入的条件可以是( )

| A. | n≤8? | B. | n≤9? | C. | n≤10? | D. | n≤11? |
11.函数f(x)的定义域为(0,1],则函数f(lg$\frac{{x}^{2}+x}{2}$)的定义域为( )
| A. | [-1,4] | B. | [-5,-2] | C. | [-5,-2]∪[1,4] | D. | [-5,-2)∪(1,4] |
1.设等差数列{an}满足:$\frac{{{{sin}^2}{a_2}-{{cos}^2}{a_2}+{{cos}^2}{a_2}{{cos}^2}{a_7}-{{sin}^2}{a_2}{{sin}^2}{a_7}}}{{sin({a_4}+{a_5})}}=1$,公差$d∈(-\frac{1}{2},0)$若当且仅当n=11时,数列{an}的前n项和Sn取得最大值,则首项a1的取值范围是( )
| A. | $(\frac{10}{11}π,π)$ | B. | $[\frac{10}{11}π,π)$ | C. | $[π,\frac{11}{10}π)$ | D. | $(π,\frac{11}{10}π)$ |
8.等差数列{an}的前n项和为Sn,已知am-1+am+1-am2=0,S2m-1=38,则m=( )
| A. | 2 | B. | 9 | C. | 10 | D. | 19 |
5.i2015的值为( )
| A. | i | B. | -1 | C. | -i | D. | 1 |
6.已知i是虚数单位,若(1+i)2-$\frac{a}{i}$是实数,则实数a的值是( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |