题目内容
2．若不等式x-1≥m（x2-1）对满足|m|≤1的所有m都成立，则x的取值范围是{1}．分析 将不等式x-1≥m（x2-1）化为含参数x的m的一次不等式（x2-1）m-（x-1）≤0，再令f（m）=（x2-1）m-（x-1），只要f（-1）≤0，f（1）≤0即可．
解答 解：原不等式化为（x2-1）m-（x-1）≤0．
令f（m）=（x2-1）m-（x-1）（-1≤m≤1）．
则$\left\{\begin{array}{l}{f（-1）=-（{x}^{2}-1）-（x-1）≤0}\\{f（1）=（{x}^{2}-1）-（x-1）≤0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x≥1或x≤-2}\\{0≤x≤1}\end{array}\right.$，
可得x=1．
故答案为：{1}．
点评 本题主要考查将一元二次不等式转化为一元一次不等式进行求解的问题，属于中档题和易错题．
练习册系列答案
相关题目
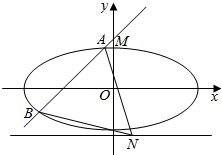已知点P（2，$\frac{\sqrt{5}}{5}$）是椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上一点，且点P在x轴上的射影恰好是椭圆C的焦点．
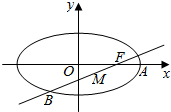椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）斜率为$\frac{b}{a}$的直线与椭圆C交于A、B两点（如图），AB中点为M，MA中点时椭圆C的右焦点F，求椭圆C的离心率e．