题目内容
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB,E为线段PB的中点,F为线段BC上的动点.

(1)求证:AE⊥平面PBC;
(2)试确定点F的位置,使平面AEF与平面PCD所成的锐二面角为30°.
【答案】(1)见解析(2)当点F为BC中点时,平面AEF与平面PCD所成的锐二面角为30°
【解析】
(1)证明![]() .
.![]() ,推出
,推出![]() 平面
平面![]() .得到
.得到![]() .证明
.证明![]() ,得到
,得到![]() 平面
平面![]() .然后证明平面
.然后证明平面![]() 平面
平面![]() .
.
(2)分别以![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立如图所示的空间直角坐标系
轴的正方向,建立如图所示的空间直角坐标系![]() ,设正方形
,设正方形![]() 的边长为2,求出为平面
的边长为2,求出为平面![]() 的法向量,平面
的法向量,平面![]() 的法向量,利用空间向量的数量积求解即可.
的法向量,利用空间向量的数量积求解即可.
解:(1)∵PA⊥平面ABCD,BC![]() 平面ABCD
平面ABCD
∴PA⊥BC
∵ABCD为正方形
∴AB⊥BC
又 PA∩AB=A,PA,AB![]() 平面PAB
平面PAB
∴BC⊥平面PAB
∴AE![]() 平面PAB
平面PAB
∴AE⊥BC
∵PA=AB,E为线段PB的中点
∴AE⊥PB
又 PB∩BC=B,PB,BC![]() 平面PBC
平面PBC
∴AE⊥平面PBC
(2)以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,
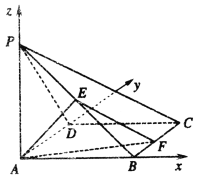
设正方形ABCD的边长为2,则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0)P(0,0,2)E(1,0,1)
∴![]() ,
,![]() ,
,![]()
设F(2,λ,0)(0≤λ≤2),
∴![]()
设平面AEF的一个法向量为![]()
则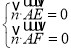
∴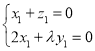
令y1=2,则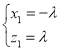
∴![]()
设平面PCD的一个法向量为![]()
则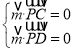
∴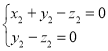
令y2=1,则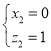
∴![]()
∵平面AEF与平面PCD所成的锐二面角为30°,
∴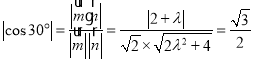 ,
,
解得λ=1,
∴当点F为BC中点时,平面AEF与平面PCD所成的锐二面角为30°

【题目】端午节是我国民间为纪念爱国诗人屈原的一个传统节日.某市为了解端午节期间粽子的销售情况,随机问卷调查了该市1000名消费者在去年端午节期间的粽子购买量(单位:克),所得数据如下表所示:
购买量 |
|
|
|
|
|
人数 | 100 | 300 | 400 | 150 | 50 |
将烦率视为概率
(1)试求消费者粽子购买量不低于300克的概率;
(2)若该市有100万名消费者,请估计该市今年在端午节期间应准备多少千克棕子才能满足市场需求(以各区间中点值作为该区间的购买量).