题目内容
【题目】已知等比数列{an}的前n项和为Sn,a1=1,且4Sn,3Sn+1,2Sn+2成等差数列.
(1)求{an}的通项公式;
(2)若数列{bn}满足b1=0,bn+1﹣bn=1,设cn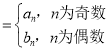 ,求数列{cn}的前2n项和.
,求数列{cn}的前2n项和.
【答案】(1)an=2n﹣1,n∈N*(2)![]() n2
n2
【解析】
(1)运用等差数列的中项性质可得3Sn+1=2Sn+Sn+2,即2an+1=an+2,根据等比数列的定义,通项公式可求;
(2)由等差数列的定义和通项公式,可得bn,求得cn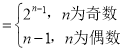 ,运用数列的分组求和,以及等差数列和等比数列的求和公式,可得所求和.
,运用数列的分组求和,以及等差数列和等比数列的求和公式,可得所求和.
解:(1)由4Sn,3Sn+1,2Sn+2成等差数列,
可得6Sn+1=4Sn+2Sn+2,即3Sn+1=2Sn+Sn+2,
即2(Sn+1﹣Sn)=Sn+2﹣Sn+1,
即2an+1=an+2,又{an}为等比数列,所以等比数列{an}的公比为2,
又a1=1,可得an=2n﹣1,n∈N*;
(2)由b1=0,bn+1﹣bn=1,可得{bn}是首项为0,公差为1的等差数列,
则bn=n﹣1,n∈N*,
cn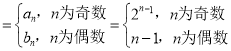 ,
,
所以{cn}的前2n项和为c1+c2+…+c2n=(a1+a3+…+a2n﹣1)+(b2+b4+…+b2n)
=(1+4+16+…+22n﹣2)+(1+3+…+2n﹣1)
![]() n
n![]() n2.
n2.

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】为了解高新产业园引进的甲公司前期的经营状况,市场研究人员对该公司2019年下半年连续六个月的利润进行了统计,统计数据列表如下:
月份 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
月利润(万元) | 110 | 130 | 160 | 150 | 200 | 210 |
(1)请用相关系数说明月利润y(单位:万元)与月份代码x之间的关系的强弱(结果保留两位小数),求y关于x的线性回归方程,并预测该公司2020年1月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,己知生产新型材料的乙企业对A、B两种型号各100件新型材料进行模拟测试,统计两种新型材料使用寿命频数如下表所示:
使用寿命 材料类型 | 1个月 | 2个月 | 3个月 | 4个月 | 总计 |
A | 15 | 40 | 35 | 10 | 100 |
B | 10 | 30 | 40 | 20 | 100 |
现有采购成本分别为10万元/件和12万元/件的A、B两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,不同类型的新型材料损坏的时间各不相同,经甲公司测算,平均每件新型材料每月可以带来5万元收入,不考虑除采购成本之外的其他成本,假设每件新型材料的使用寿命都是整数月,且以频率估计每件新型材料使用寿命的概率,如果你是甲公司的负责人,以每件新型材料产生利润的期望值为决策依据,你会选择采购哪款新型材料?
参考公式:相关系数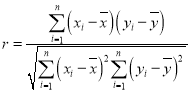 ;
;
回归直线方程为![]() ,其中
,其中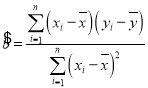 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.