题目内容
【题目】如图，在直三棱柱
中，
，
,
分别是
,
的中点．
（1）求证：
∥平面
；
（2）求证：平面
平面
．
【答案】（Ⅰ）详见解析（Ⅱ）详见解析
【解析】
试题分析：（Ⅰ）证明线面平行，一般利用线面平行判定定理，即从线线平行出发给予证明，而线线平行的寻找与论证，往往需要结合平几知识，如三角形中位线性质，及利用柱体性质，如上下底面对应边相互平行（Ⅱ）证明面面垂直，一般利用面面垂直判定定理，即从线面垂直出发给予证明，而线面垂直的证明，往往需要利用线面垂直判定与性质定理进行多次转化：由直棱柱性质得侧棱垂直于底面：
底面
，再转化为线线垂直
；又根据线线平行
，将线线垂直
进行转化
，再根据线面垂直判定定理得
平面
试题解析：证明：（1）因为
,
分别是
,
的中点，所以， ...........2分
又因为在三棱柱
中，
，所以
. ...............4分
又
平面
，
平面，所以
∥平面. ...............6分
（2）在直三棱柱中，
，
又
底面，所以. .............8分
又，，所以， ..........10分
又
平面，且
，所以平面. ...............12分
又
平面
，所以平面
平面
． ............14分
（注：第（2）小题也可以用面面垂直的性质定理证明平面，类似给分）
【题目】某险种的基本保费为a(单位：元)，继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件：“一续保人本年度的保费不高于基本保费”，求P(A)的估计值；
(2)记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160%”，求P(B)的估计值；
(3)求续保人本年度平均保费的估计值．
【题目】某校高三年级共有学生
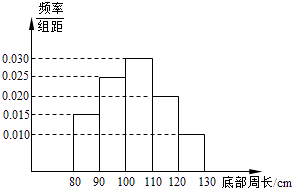
名，为了解学生某次月考的情况，抽取了部分学生的成绩（得分均为整数，满分为
分）进行统计，绘制出如下尚未完成的频率分布表：
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
| |
| ||
|
|
（1）补充完整题中的频率分布表；
（2）若成绩在
为优秀，估计该校高三年级学生在这次月考中，成绩优秀的学生约为多少人.
